午後わてんのブログ

ベランダ菜園とWindows用アプリ作成(WPFとC#)

画像にノイズ付加するアプリ、一様分布乱数から正規分布乱数生成、エクセルのNORMINV関数で正規乱数

WPF、C# .NET #ソフトウェア WPF ↓Windows用アプリ 画像処理 エクセルExcel2007 算数
画像にノイズ付加してみた
ピクセルの輝度値に乱数を加えればノイズになる
一様分布になる乱数と正規分布になる乱数、正規乱数
 
一様分布
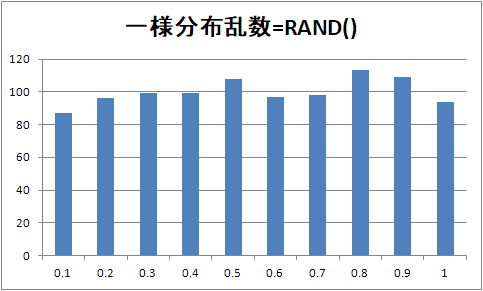
イメージ 1
エクセルのRAND関数の結果1000個のヒストグラム
どの範囲もだいたい同じ個数になっている、こういうのを一様分布っていうみたい
エクセルのRAND関数や.NET FrameworkのSystem.Randomクラスから得られる乱数はこれ
それに対して正規乱数は
 
イメージ 2
正規分布になる乱数を正規乱数とかいうみたい
この正規乱数(に近いもの)を生成する方法がいくつかあって今回は
  • 乱数を12回足して6引く
  • ボックス=ミュラー法
この2つを使ってみた
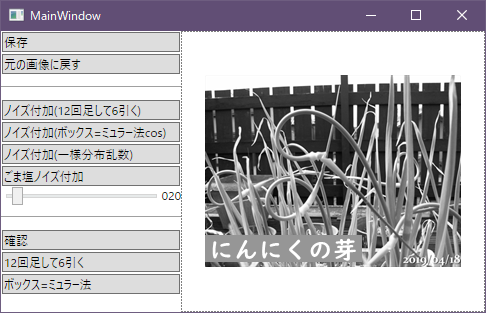
イメージ 3
 
 
元画像はいつもの
イメージ 4
これにノイズ付加
 
イメージ 5
上の2つは正規乱数生成法が違うだけど標準偏差20と同じなので結果もほぼ同じ、結構ジャリジャリになるんだなあ
左下は普通の乱数-20～20で生成したのを元の輝度値に足して作成、これも思っていたよりジャリジャリになった、それでも正規乱数よりもノイズが少ない、これは標準偏差20の正規乱数だと乱数の幅が-20～20よりも大きくなるからだろうねえ
7.8%のごま塩、これもごま塩多いなあって印象
 
 
 
 
 
 
 
ごま塩ノイズ
元の輝度値に関係なく0(黒)か255(白)にするだけなので、普通の乱数を使っている
10%のごま塩なら白と黒を5%づつ作るだけ

f:id:gogowaten:20191214125130p:plain

209行目、乱数がしきい値以下ならごま塩にする
211行目、乱数が0.5未満なら0(黒)、以上なら255(白)
 
 
普通の乱数

f:id:gogowaten:20191214125140p:plain

178行目、元の輝度値(pixels[p])に指定幅(noise)の乱数を足す
 
 
 
 
 
 
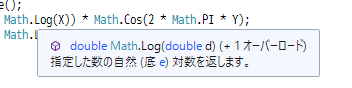
正規乱数生成
普通の乱数を12回足して6引く方法
 
この方法でできるのは正規乱数ではなくて、正規乱数に近い乱数らしい
どれくらい近いのかエクセルのRAND関数で試してみた

f:id:gogowaten:20191214125151p:plain

グラフの形見ると完璧じゃん！ってくらいのができている
 

f:id:gogowaten:20191214125204p:plain

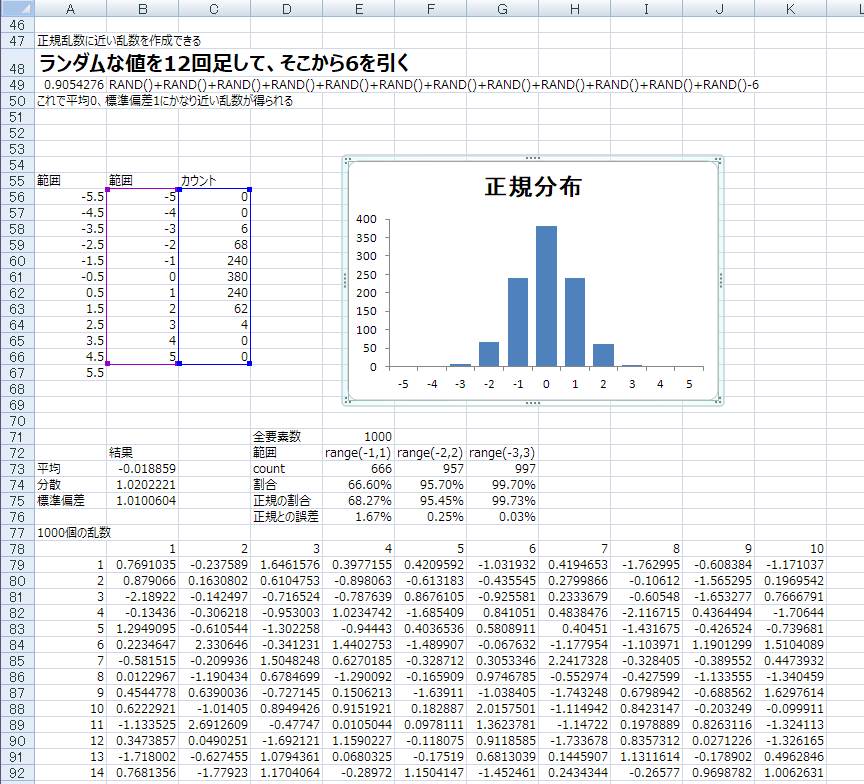
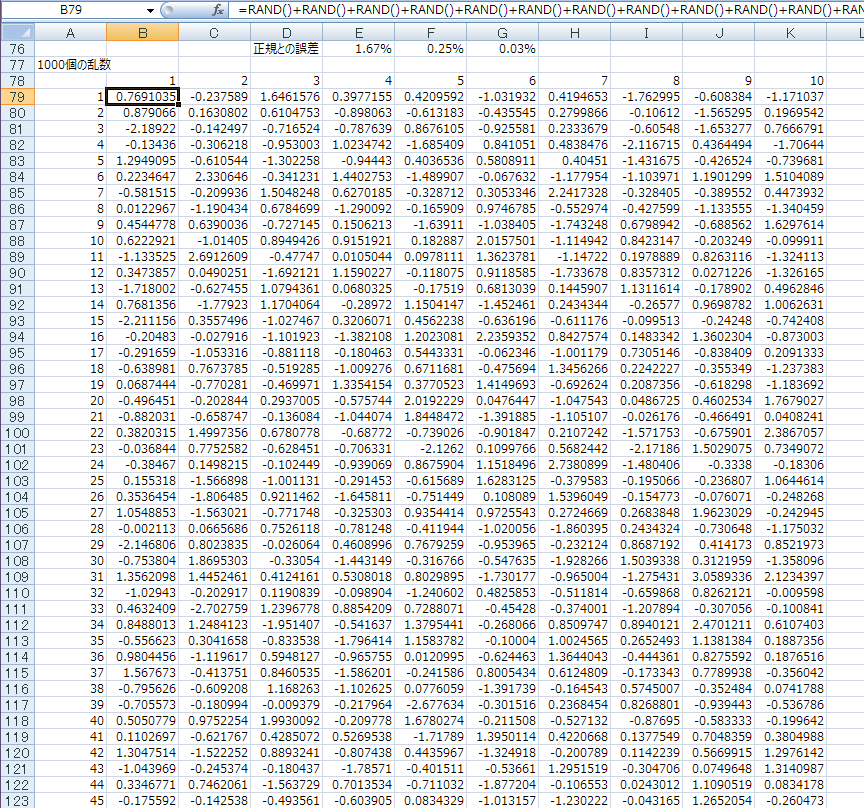
1000個のセルに
=RAND()+RAND()+RAND()+RAND()+RAND()+RAND()+RAND()+RAND()+RAND()+RAND()+RAND()+RAND()-6
って入れて
 

f:id:gogowaten:20191214125215p:plain

0.1範囲ごとにカウントして
 

f:id:gogowaten:20191214125226p:plain

グラフに、きれいな正規分布になっている
 
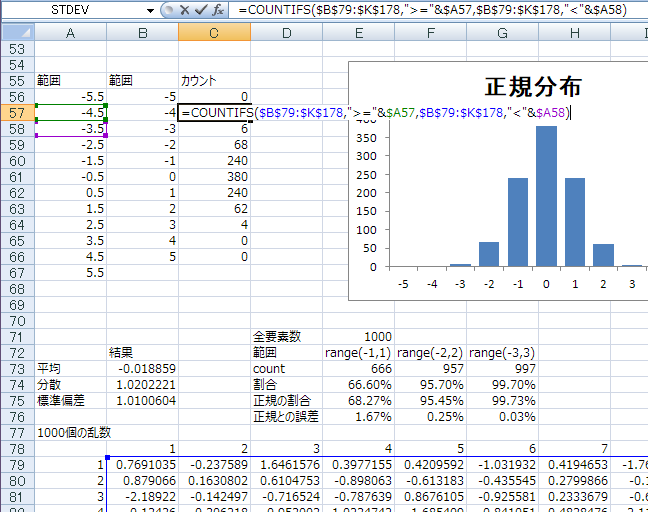
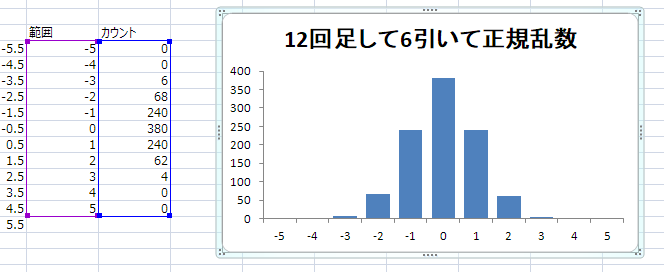
再計算

f:id:gogowaten:20191214125243p:plain

多少ずれたりもするけどこの程度
 
 
 
イメージ 15
標準正規分布は平均が0、標準偏差が1
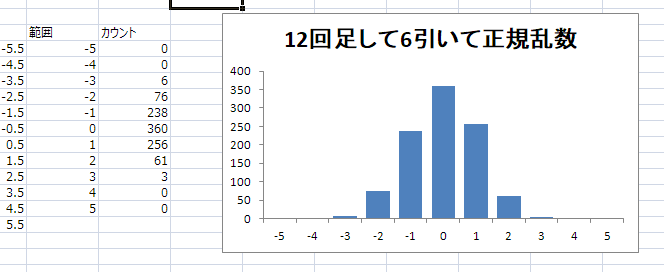
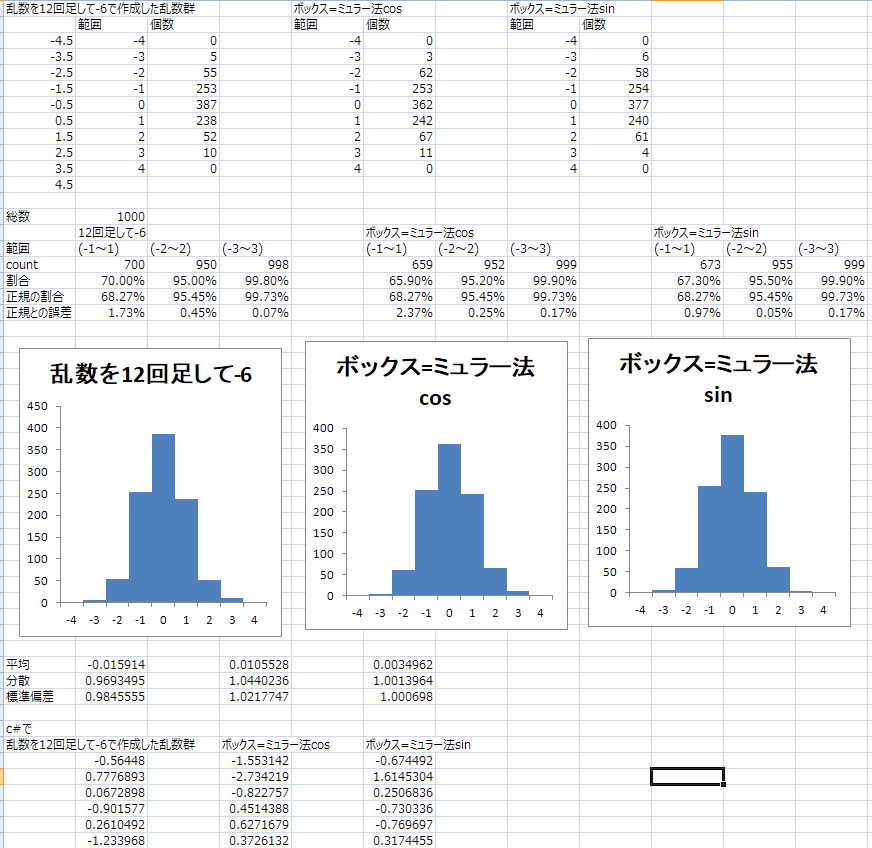
得られた乱数での結果は平均が0.025、標準偏差は1.022
ほとんど差がなく、これもいい結果
 
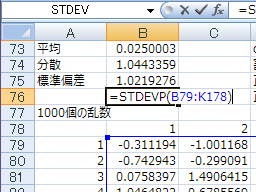
イメージ 14
標準偏差はSTDEVP関数で
 
 
標準正規分布では-1から1までの範囲に要素の68.27%が入る
-2～2の範囲には95.45%
-3～3の範囲には99.73%ってことなので、これとも比較
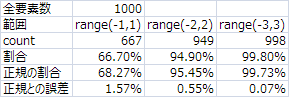
イメージ 16
1.57%の誤差は大きい気もするけど要素数が少ないからかもねえ
でも十分だと思う
 
 
 
 
 
ボックス=ミュラー法
イメージ 18
イメージ 19
これでできるらしい
 
XとYにそれぞれ別の普通の乱数を入れて計算、つまり1つ作るときでも2つの乱数が必要
logは対数、自然対数とからしい、よくわからんけどエクセルにはそれに相当するLOG関数がある、.NET Frameworkにもあるので安心
2つ式があるけど、両方使う必要はない？よくわからんけどたくさん生成するなら2つの乱数から1つを作るより、ついでに2つ作ったほうがいいのかも
 
エクセルだと
Z1=SQRT(-2*LOG(RAND(),EXP(1)))*COS(2*PI()*RAND())
Z2=SQRT(-2*LOG(RAND(),EXP(1)))*SIN(2*PI()*RAND())
 
エクセルで試した結果

f:id:gogowaten:20191214125300p:plain

グラフの形を見るとイマイチな気もするけど正規分布になっていると思う
 

f:id:gogowaten:20191214125312p:plain

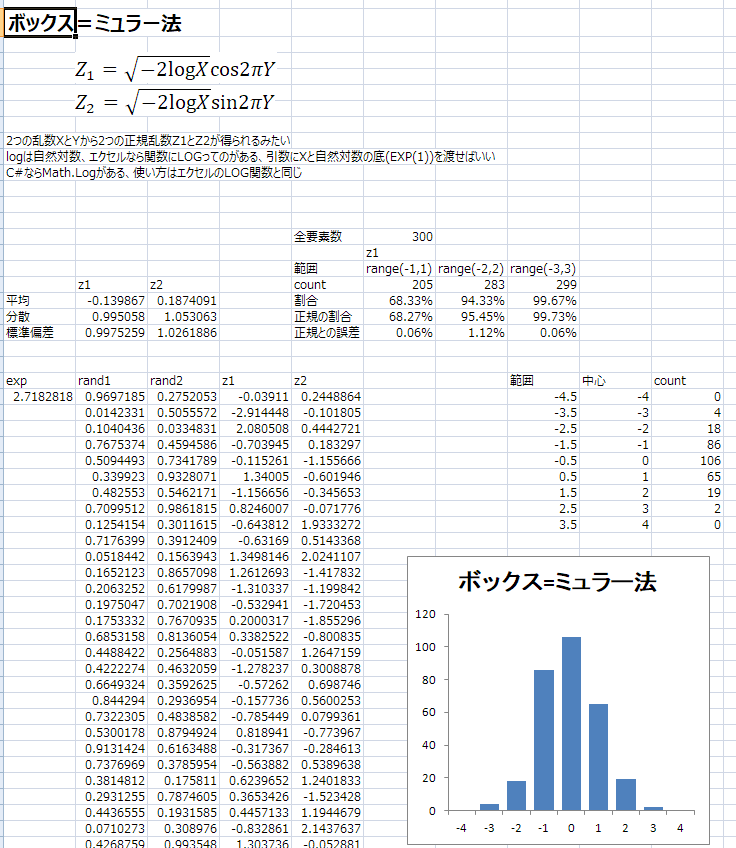
LOG関数

f:id:gogowaten:20191214125346p:plain

=LOG(256,2)、この結果は8になる
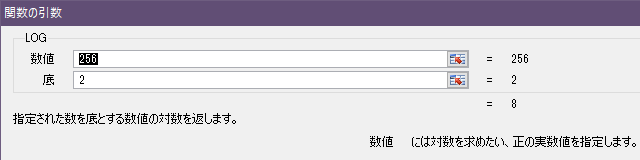
2の8乗＝256
今回の式ではLOG関数の第2引数には自然対数の底を指定する
エクセルだとEXP関数に1を渡したのが自然対数の底になるので
LOG(数値、EXP(1))
 
 
 
 
 
 
 
 
 
 
 
 
 
c#でSystem.Randomの乱数から
普通の乱数を12回足して6引く方法で、指定した個数乱数を作成
イメージ 8
 
ボックス=ミュラー法で正規乱数作成
イメージ 23
Math.Log関数
イメージ 24
C#にもLog関数あった
 
 
1000個作成
イメージ 17
一時停止して値をエクセルにコピペ
 
結果

f:id:gogowaten:20191214125422p:plain

どれもいい結果になった
 
エクセルではイマイチな気もしたボックス=ミュラー法、C#では良くなっているように見える
それでも12回足して6引くほうがきれいかなあ
ボックス=ミュラー法はコサイン使うのとサイン使うのがあるけど、どちらも同じ感じだった
 
 
 
エクセルには正規分布関数NORMDIST関数の逆関数NORMINV関数がある
イメージ 26
これもよくわからんけど逆関数っていう名前的に、結果の値からもとの値を求める感じかしら
第1引数の確率に乱数を入れて、平均と標準偏差には標準正規分布の値を入れると
 

f:id:gogowaten:20191214125437p:plain

多分これが一番正規乱数だと思います
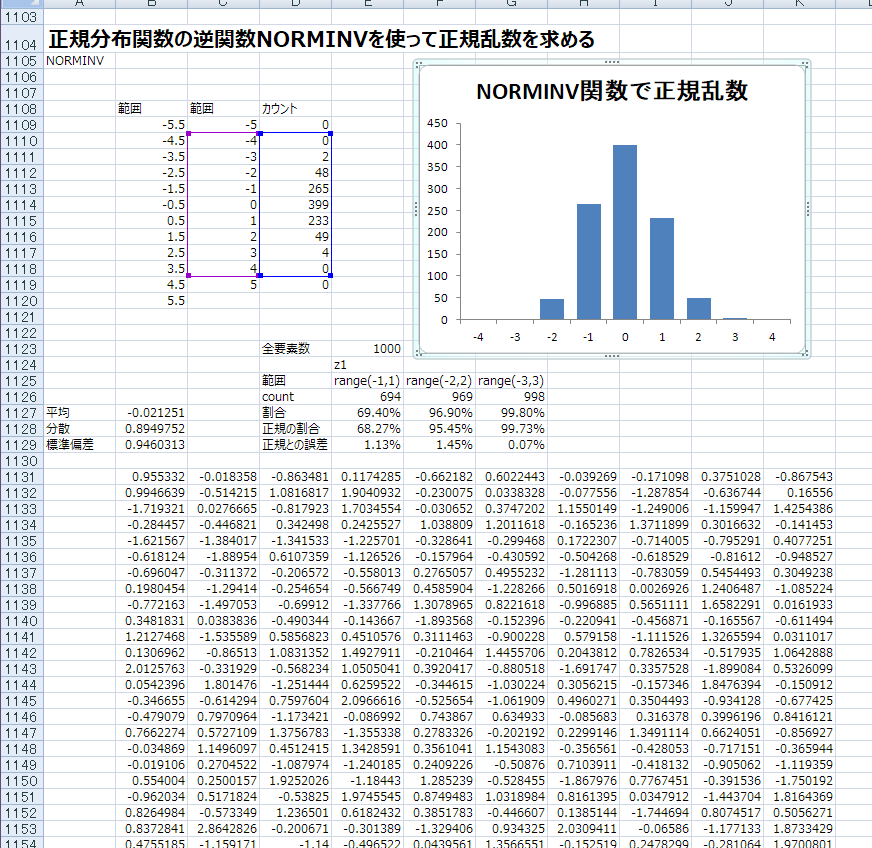
それでもグラフを見ると他の生成法と同じくらいずれている
ってことは1000個くらいだとこれくらいずれるってことかな
逆に言うと12回足して6引く方法も、ボックス=ミュラー法も実質正規乱数
エクセルは何でも揃っているなあ
 
 
 
得られた正規乱数で画像の輝度を変化させる
 
元の輝度が200
得られた乱数が0.9
標準偏差を40に指定
この場合は236になる
 
40*0.9+200=236
これは
 
標準偏差＊乱数＋元の輝度
 
 
切り捨てと切り上げ
標準偏差を100に指定して、それ以外が同じだと
100*0.9+200=290
輝度の最大値は255なので290は255に切り捨てる
同じように結果が0未満だったときは0に切り上げる
 
 
12回足して6引く方法の乱数で輝度変化(ノイズ付加)

f:id:gogowaten:20191214125449p:plain

107～115行目、乱数生成
125行目、標準偏差＊乱数＋元の輝度
 
 
 
ボックス=ミュラー法でノイズ付加

f:id:gogowaten:20191214125502p:plain

乱数生成の140～146行目以外はさっきと同じ
 
 
 
表示画像の平均輝度、分散、標準偏差の表示

f:id:gogowaten:20190922173019p:plain

輝度値の配列pixelsから計算して表示
 
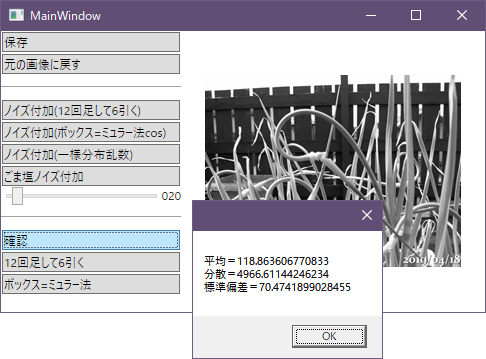
イメージ 31
この画像の輝度平均は119
標準偏差は70.5だった
 
標準偏差100、12回足して6引く
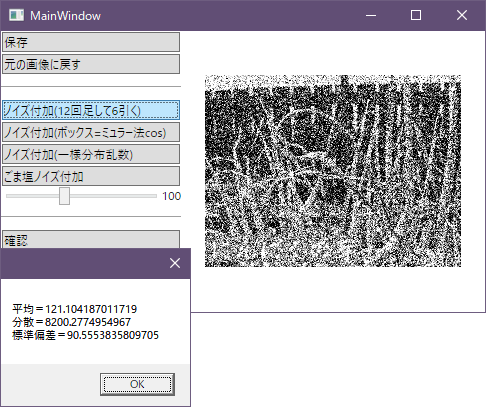
イメージ 32
平均輝度121
標準偏差＝90.6
 
 
標準偏差100でボックス=ミュラー法
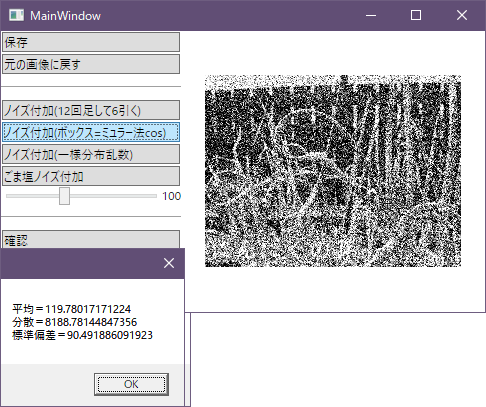
イメージ 33
平均輝度120
標準偏差＝90.5
やっぱりさっきのとほとんど同じ
 
 
元の輝度値に-100～100の普通の乱数を加算
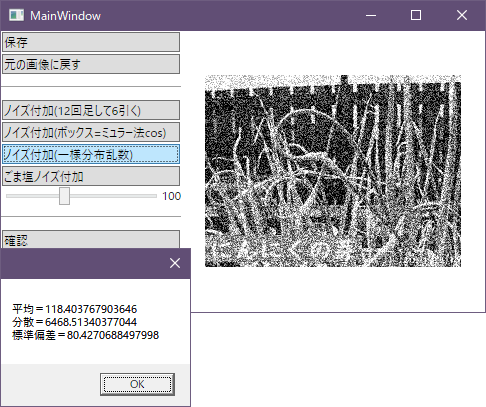
イメージ 34
平均輝度118
標準偏差＝80.4
少しおとなしくなる
正規乱数なら-3～3の範囲に99.73%
 
つまりほとんど全部
標準正規分布なら範囲ごとに含まれる要素の割合が
-1～1 -2～2 -3～3
68.27% 95.45% 99.73%
ということなので
普通乱数で-100～100ってのは
標準偏差100の正規乱数の-1～1の範囲、これは68.27%しか当てはまらないことになる
じゃあ普通乱数で-200～200にすれば、正規乱数だと-2～2に相当するから95.45%と範囲だけならほぼ同等になる
 
普通乱数で-200～200
イメージ 35
普通乱数は一様分布だから両極端な値も同確率で出るから
よりノイズが大きくなる
 
イメージ 36
 
イメージ 37
 
一様分布乱数の範囲に使う数値の半分を、正規乱数の標準偏差の半分にすると、似たようなノイズになるかなあ
これなら正規乱数を使わなくても、普通の一様分布乱数でいいような気がする
 
 
 
処理時間
体感だと
12回足して6引く ＞＞ ボックス=ミュラー法 ＞＞ 一様分布乱数 ＞ ごま塩ノイズ
 
2048ｘ1536ピクセルの画像だと
1秒、0.5秒、0.2秒、0.1秒
こんな体感
ボックス=ミュラー法が一番重い処理かなと予想したけど、12回足して6引くのほうが2倍くらい重かった、一様分布でも乱数は乱数だから結構重たいのかしらねえ
 
 
 
イメージ 39
輝度値192の画像
これに少しのノイズを付加
 
イメージ 38
 
 
今回のフォントは初心に返って
イメージ 40
HGP創英角ポップ体
 
 
 
 
 
Compression Technology of Image Data
http://www.comp.tmu.ac.jp/morbier/imagproc/imageconvert.html
ここを見て画像にノイズ付加を試してみようと思ったんだけど
12回足して6引く方法を使っていて、これが何なのかさっぱりわかんなかった
ここに書いてある正規分布乱数でググればよかったんだけど、それが鍵になっているってのに気づかなくて、"画像にノイズ付加"とかでググっているうちに
ガウシアンノイズ(正規分布ノイズ)、ホワイトノイズ、ホワイトガウスノイズ、正規乱数ってのが出てきて
正規分布になる乱数が正規乱数っていうみたい、これが重要
普通の乱数(System.Random)は一様分布
普通の乱数を12回足して6引くと正規乱数に近いものが得られるってのを見つけて、理屈は理解できなかったけどこれだったのかと
ノイズ付加するだけでも難しいねえ、ごま塩ノイズは簡単だけどね
 
RANDOM……お決まりの乱数……一様分布乱数12個から生成する疑似正規乱数……中心極限定理……理解しようなんていうおとぎ話は始まってすらいない……ごま塩ノイズ程度に覚えておいてくれ……
 
 
参照したところ
レーシングポエムったー
https://shindanmaker.com/137465
こんな診断メーカーがあるのかよ……冗談じゃねえ……
 
 
 
Box-Muller法による正規分布列生成 - Qiita
https://qiita.com/mude/items/8c8b24b1404facfd3c03
 
自然対数・常用対数・二進対数の使い分け。log,ln,lg,expはどういう意味？ | アタリマエ！
https://atarimae.biz/archives/12731
 
 
一様乱数から正規乱数を作る方法？ | 配電盤
http://blog.unfindable.net/archives/7097
 
平均値から正規分布乱数を生成する方法（PHP） | colori
https://colo-ri.jp/develop/2017/10/gausian-rand-from-average.html
 
 
C#でボックスミューラー法による正規分布に従う乱数生成 - 真実の楽譜（フルスコア）
http://truthfullscore.hatenablog.com/entry/2014/06/03/204446
 
正規乱数・正規分布する乱数を発生させる－NORMINV関数・RAND関数:Excel(エクセル)の関数・数式の使い方-数学
https://www.relief.jp/docs/003097.html
 
 
 
 
 
ギットハブ

github.com

 
アプリダウンロード先

github.com

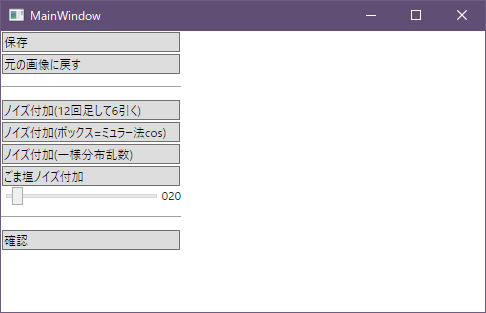
イメージ 41
画像ファイルドロップで画像表示
ノイズの強さをスライダーで決めて、ノイズ付加のボタンでノイズ付加
ノイズの重ねがけできる
画像のクリックで元の画像と切り替えて比較できる
 
 
関連記事
次回、2019/05/24は2日後

gogowaten.hatenablog.com

画像にノイズ付加するアプリ、カラー版 ( ソフトウェア ) - 午後わてんのブログ - Yahoo!ブログ
https://blogs.yahoo.co.jp/gogowaten/15962326.html
 
2019/4/27は3週間前

gogowaten.hatenablog.com

エクセルで1次のガウス関数(確率密度関数)、正規分布関数のNORMDIST ( ソフトウェア ) - 午後わてんのブログ - Yahoo!ブログ
https://blogs.yahoo.co.jp/gogowaten/15942730.html
メディアンフィルタで画像のノイズ除去試してみた、WPF、C# ( ソフトウェア ) - 午後わてんのブログ - Yahoo!ブログ
https://blogs.yahoo.co.jp/gogowaten/15965377.html