C#で累積分布関数っぽいの、配列の値から作った正規分布の指定区間の面積(割合)を台形の面積で求めてみた

正規分布の面積

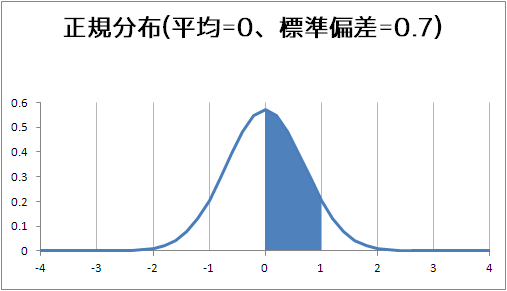
x(横軸)が0～1までの塗りつぶしてあるところの面積が、全体の何%なのかを知りたい
エクセル2007ならNORMDIST関数を使えばラクにできる、新しいエクセルならもっとラクかも
平均=0、標準偏差=0.7のときxが0～1までの面積の割合は
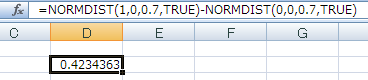
=NORMDIST(1,0,0.7,TRUE)-NORMDIST(0,0,0.7,TRUE)
=0.4234363なので約42.3%

NORMDIST関数の4つ目の引数

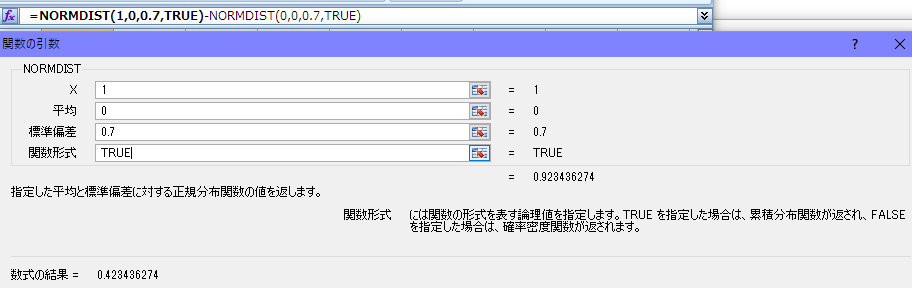
NORMDIST関数の4つ目の引数にTRUEを渡すと、累積分布関数ってのが返ってくる
これはどうやらxの値がマイナスに無限？から1つ目の引数にしていした値までの累積の確率？が返ってくるみたいで、さっきと同じ条件のときxに1を指定した場合は、0.923436274が返ってくる、これは全体の92.3436274%
グラフにすると多分こんな感じ

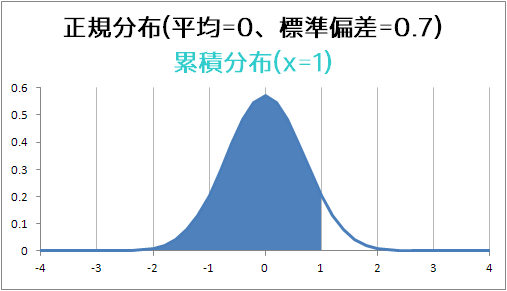
塗りつぶしてあるところが全体の92.3436274%、グラフのずっと左から1までの累積ってことみたい、なので0～1の間の面積は1のときの面積-0のときの面積で得られるのが最初の
=NORMDIST(1,0,0.7,TRUE)-NORMDIST(0,0,0.7,TRUE)
この引き算をグラフでみると

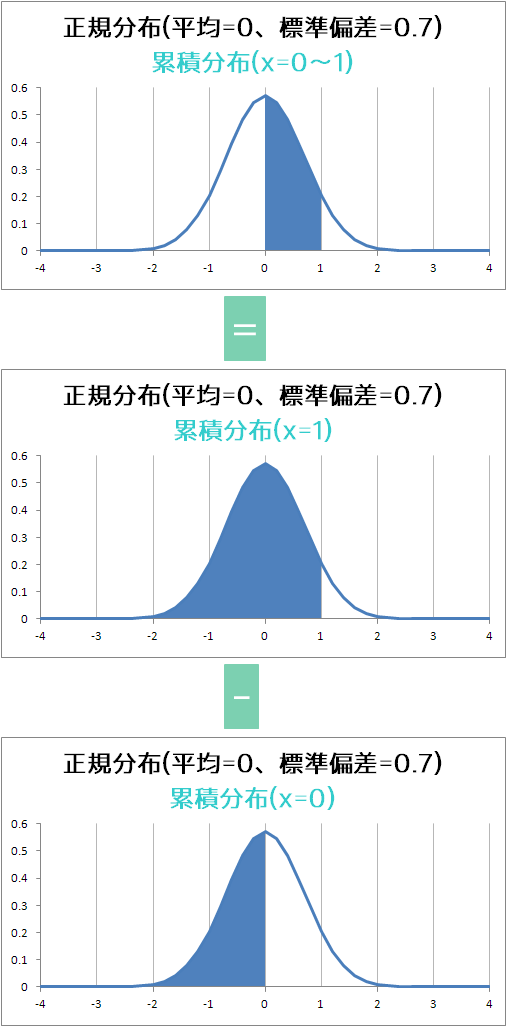
こんなイメージ






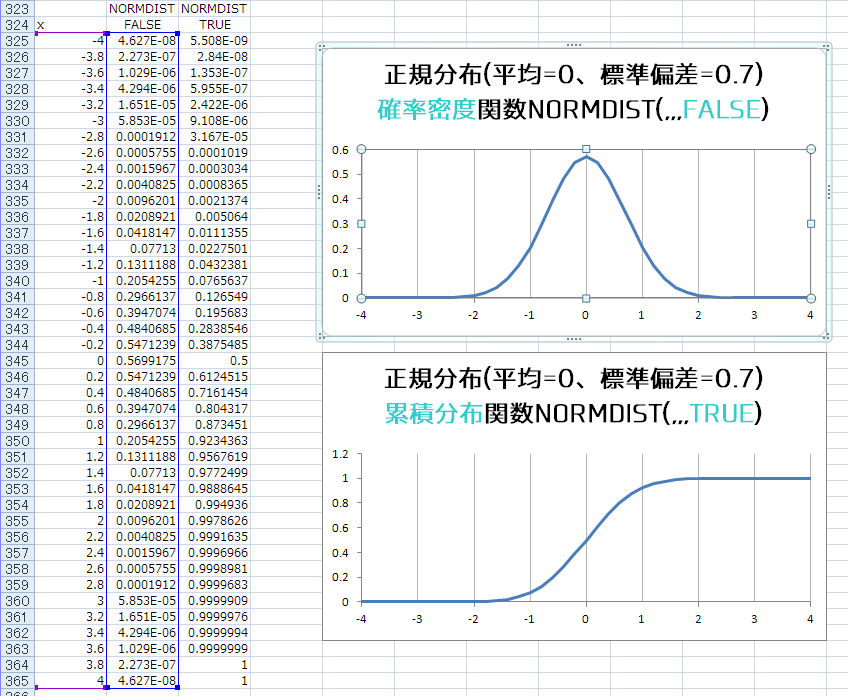
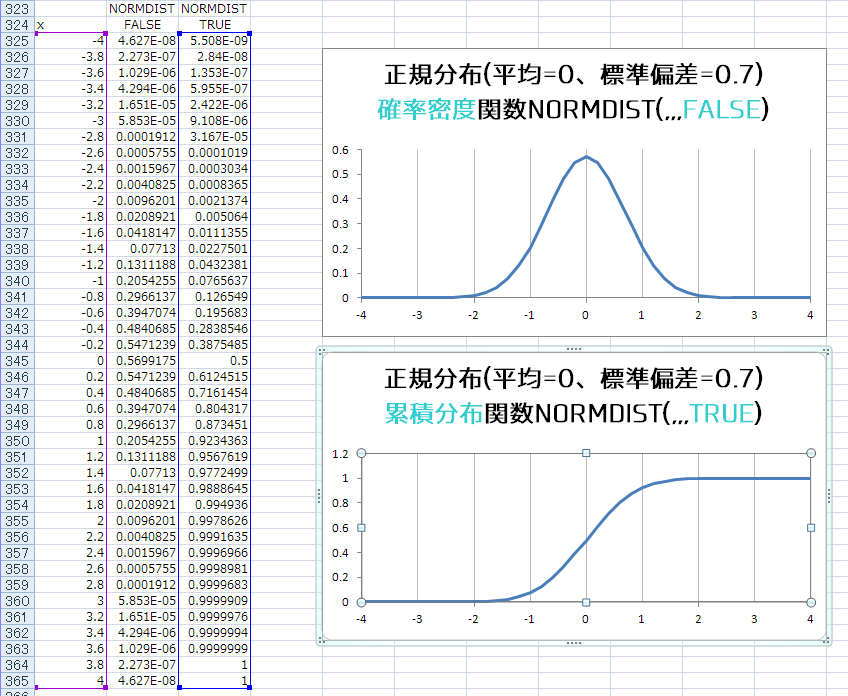
エクセルではNORMDIST関数にTRUEでできた、次はC#…は全くわからなかったので
blog.goo.ne.jp こちらを参考にして、というかほとんど同じなんだけど

台形の面積で計算していく

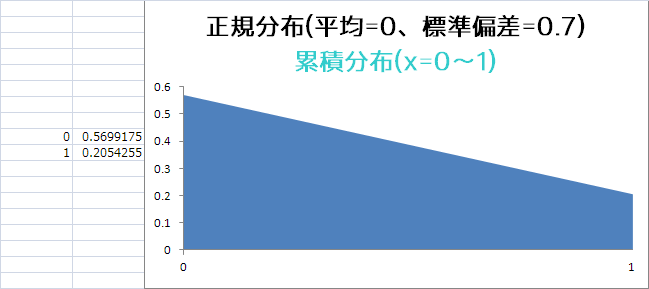
xを1刻みにして0～1を見ると台形になる、台形の面積は
(上底＋下底)x高さ/2
0が0.5699175
1が0.2054255
このどちらかをそれぞれ上底下底にしてxの差を高さにすればいいから計算したら
(0.5699175+0.2054255)x(1-0)/2=0.3876715
NORMDIST＋TRUEで計算したときは0.4234363だったから随分違う

0.1刻みにして計算

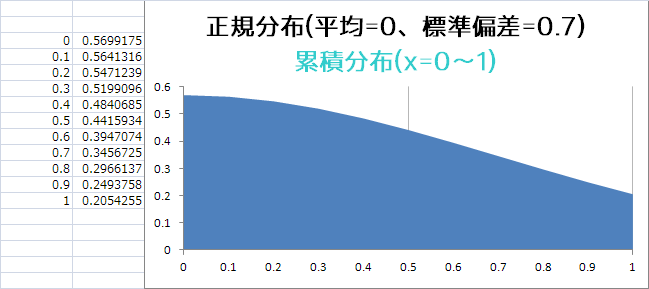
これの0.1刻みごとの台形を計算して足していく


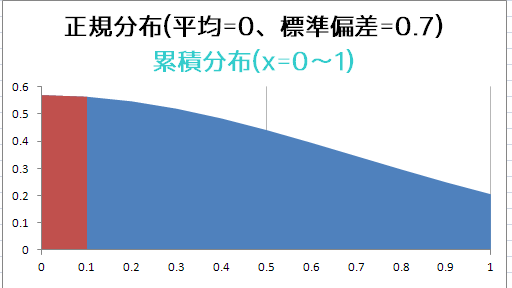
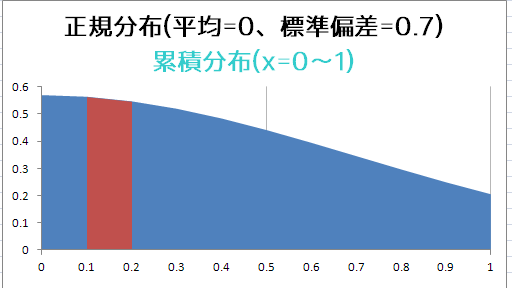
0.1刻みなのでより正確になる

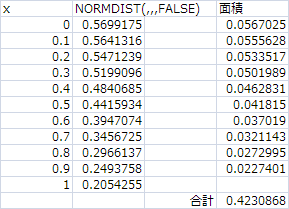
結果は0.4230868になった。NORMDISTと比較しても0.4230868-0.4234363=-0.0003495とかなり近くなった

配列の値から正規分布
正規分布はエクセルのNORMDIST関数を見ると、平均値と標準偏差があればできる感じなので
int vs = new int { 3, 4, 0, 0, 0, 1, 1, 4, 0, 1, 2, 2, 3, 0, 3, 3, 0, 0, 4, 4 };
っていう配列から作ってみるまえに、やっぱりエクセルで確認

こんな感じの20個のセルの値からヒストグラムにしてみると

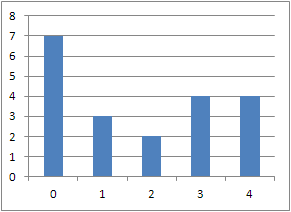
こうで、セルに書いてみると

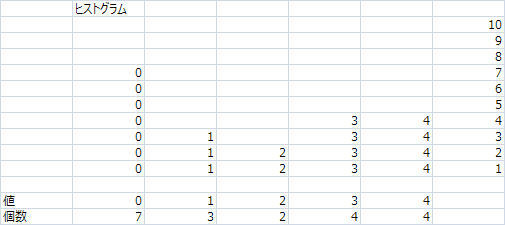
こう

平均値は1.75、標準偏差は1.577181

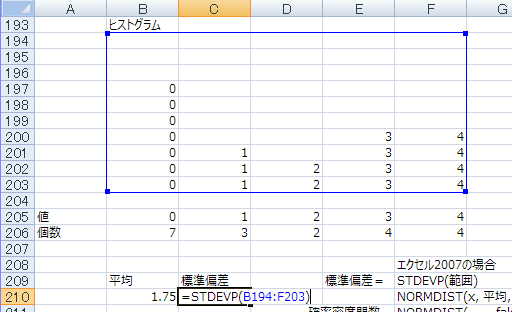
STDEVPで標準偏差が得られる

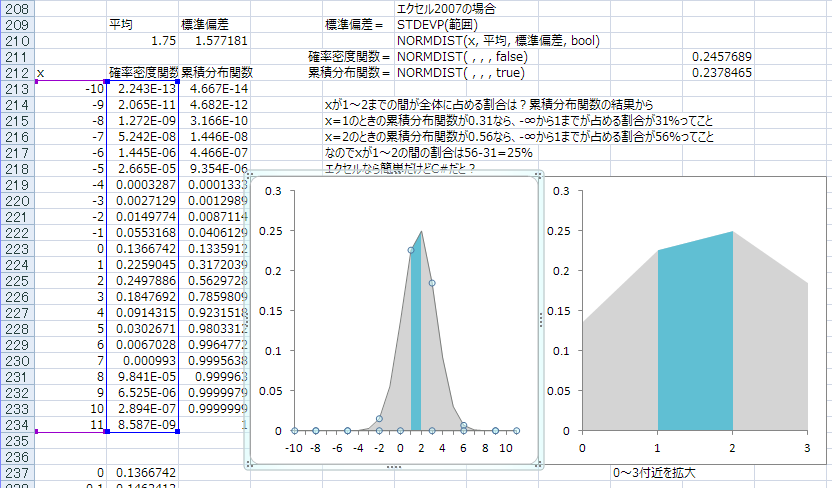
得られた平均値と標準偏差をNORMDIST関数に入れてみてグラフにしたら正規分布のグラフになった、これであっているのか意味があるのかもわかんないけど、できた。これから1～2の面積を求めたい、エクセルの累積分布関数でみると1と2それぞれは
0.317203926
0.562972788
なので0.562972788-0.317203926=0.24576886が答え、これを目指したい
C#に戻って
必要な計算は

• 平均値
  
• 標準偏差
  
• 確率密度関数
  
• 台形の面積
  

平均値はいいとして、標準偏差、標準偏差を2乗したのが分散で、確率密度関数では標準偏差を2乗するから分散があればいいってことになる

//分散 = 2乗の平均 - 平均の2乗
private double Variance(int[] vs, double average)
{
    int total = 0;
    foreach (var item in vs)
    {
        total += item * item;
    }
    //2乗の平均 - 平均の2乗
    return ((double)total / vs.Length) - (average * average);
}

確率密度関数

/// <summary>
/// 確率密度関数
/// </summary>
/// <param name="x"></param>
/// <param name="average">平均</param>
/// <param name="variance">分散(標準偏差^2)</param>
/// <returns></returns>
private decimal ProbabilityDensity(decimal x, double average, double variance)
{
    if (variance == 0)
        return 0m;
    double xa = (double)x - average;
    double ei = -(xa * xa / (2 * variance));//expIndex
    double e = Math.Pow(Math.Exp(1), ei);
    double el = 1 / Math.Sqrt(2 * Math.PI * variance);//expLeft
    return (decimal)(el * e);            
}

これは以前の記事
gogowaten.hatenablog.com

gogowaten.hatenablog.com

この辺から
少し違うのは、前回は平均値=0、標準偏差=1の標準正規分布だったけど、今回は平均値が0以外、標準偏差も1以外になるから標準じゃない正規分布の式をつかう

これを使って

/// <summary>
/// 累積分布関数
/// </summary>
/// <param name="begin">区間開始</param>
/// <param name="end">区間終了</param>
/// <param name="average">平均値</param>
/// <param name="variance">分散(標準偏差^2)</param>
/// <param name="resolution">計算精度、区間の分割数で1000あれば十分</param>
/// <returns></returns>
private decimal CumulativeDistribution(decimal begin, decimal end, double average, double variance, decimal resolution)
{
    decimal unit = (end - begin) / resolution;
    decimal total = 0m;
    for (decimal i = begin; i < end; i += unit)
    {
        //台形面積 = (上底＋下底)＊高さ/2
        total += (ProbabilityDensity(i, average, variance) + ProbabilityDensity(i + unit, average, variance)) * unit / 2m;
    }          
    return total;
}

forのカウンタにdecimal型を使うのは見たことないけど有りなのかなあ、0.1とか0.001づつカウントしたいから最初はdouble型で計算したら微妙に誤差が出て蓄積されるから誤差の出ないdecimal型にした

実際に計算

private void Test()
{
    int[] vs = new int[] { 3, 4, 0, 0, 0, 1, 1, 4, 0, 1, 2, 2, 3, 0, 3, 3, 0, 0, 4, 4 };
    double average = vs.Average();
    var variance = Variance(vs, average);
    decimal begin = 1.0m;//区間開始点
    decimal end = 2.0m;//区間終了点
    decimal resolution = 100m;
    var vv = CumulativeDistribution(begin, end, average, variance, resolution);
    var mm = MyCalc(vs, begin, end, resolution);
}

1～2間の面積を1刻み(resolution=1)で計算した結果は

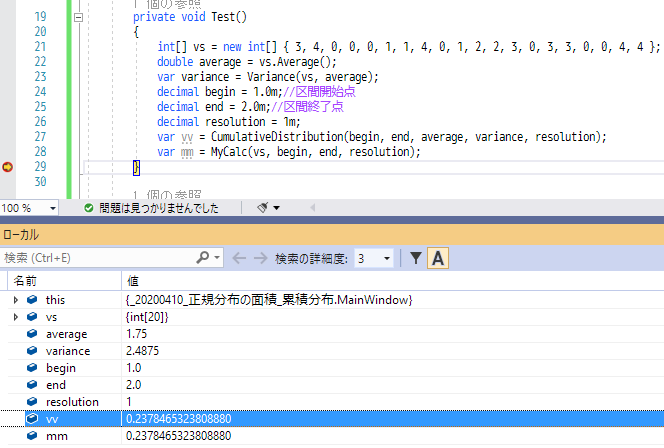
0.2378465323808880
エクセルの累積分布関数では
0.245768861
差は0.2378465323808880-0.245768861=-0.0079223286

resolution=1000にして(2-1)/1000=0.001刻みで計算だと

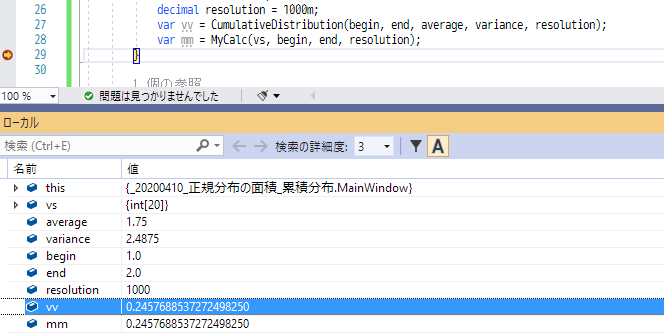
0.2457688537272498250
エクセルとの差は
0.2457688537272498250-
0.245768861=-7.2727502e-09
ほぼ0

コード全部
MainWindow.xaml

<Window x:Class="_20200410_正規分布の面積_累積分布.MainWindow"
        xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation"
        xmlns:x="http://schemas.microsoft.com/winfx/2006/xaml"
        xmlns:d="http://schemas.microsoft.com/expression/blend/2008"
        xmlns:mc="http://schemas.openxmlformats.org/markup-compatibility/2006"
        xmlns:local="clr-namespace:_20200410_正規分布の面積_累積分布"
        mc:Ignorable="d"
        Title="MainWindow" Height="450" Width="800">
    <Grid>

    </Grid>
</Window>

MainWindow.xaml.cs

using System;
using System.Linq;
using System.Windows;

//正規分布の面積

namespace _20200410_正規分布の面積_累積分布
{
    /// <summary>
    /// Interaction logic for MainWindow.xaml
    /// </summary>
    public partial class MainWindow : Window
    {
        public MainWindow()
        {
            InitializeComponent();
            Test();
        }
        private void Test()
        {
            int[] vs = new int[] { 3, 4, 0, 0, 0, 1, 1, 4, 0, 1, 2, 2, 3, 0, 3, 3, 0, 0, 4, 4 };
            double average = vs.Average();
            var variance = Variance(vs, average);
            decimal begin = 1.0m;//区間開始点
            decimal end = 2.0m;//区間終了点
            decimal resolution = 1000m;
            var vv = CumulativeDistribution(begin, end, average, variance, resolution);
            var mm = MyCalc(vs, begin, end, resolution);
        }

        private decimal MyCalc(int[] specimen, decimal begin, decimal end, decimal resolution)
        {
            double average = specimen.Average();
            var variance = Variance(specimen, average);
            return CumulativeDistribution(begin, end, average, variance, resolution);
        }

        /// <summary>
        /// 累積分布関数
        /// </summary>
        /// <param name="begin">区間開始</param>
        /// <param name="end">区間終了</param>
        /// <param name="average">平均値</param>
        /// <param name="variance">分散(標準偏差^2)</param>
        /// <param name="resolution">計算精度、区間の分割数で1000あれば十分</param>
        /// <returns></returns>
        private decimal CumulativeDistribution(decimal begin, decimal end, double average, double variance, decimal resolution)
        {
            decimal unit = (end - begin) / resolution;
            decimal total = 0m;
            for (decimal i = begin; i < end; i += unit)
            {
                //台形面積 = (上底＋下底)＊高さ/2
                total += (ProbabilityDensity(i, average, variance) + ProbabilityDensity(i + unit, average, variance)) * unit / 2m;
            }           
            return total;
        }
      
        /// <summary>
        /// 確率密度関数
        /// </summary>
        /// <param name="x"></param>
        /// <param name="average">平均</param>
        /// <param name="variance">分散(標準偏差^2)</param>
        /// <returns></returns>
        private decimal ProbabilityDensity(decimal x, double average, double variance)
        {
            if (variance == 0)
                return 0m;
            double xa = (double)x - average;
            double ei = -(xa * xa / (2 * variance));//expIndex
            double e = Math.Pow(Math.Exp(1), ei);
            double el = 1 / Math.Sqrt(2 * Math.PI * variance);//expLeft
            return (decimal)(el * e);            
        }



        //分散 = 2乗の平均 - 平均の2乗
        private double Variance(int[] vs, double average)
        {
            int total = 0;
            foreach (var item in vs)
            {
                total += item * item;
            }
            //2乗の平均 - 平均の2乗
            return ((double)total / vs.Length) - (average * average);
        }
    }
}

github.com

---

日記
エクセルのNORMDISTのTRUE指定は何に使うのかわかんなかったけど、こういうのに使うんだねえ。文系の学校だったせいもあるけど、国語より算数をもっと教えて欲しかったって思うわけ、選択肢が1つしかないのは選択じゃないって、それ一番言われてるから

関連記事
次回のWPF記事は4日後
gogowaten.hatenablog.com

前回のWPF記事は6日前
gogowaten.hatenablog.com