1次元のガウス関数をエクセルで
前回の画像のぼかし処理で使った
ガウシアンフィルタとかマスクとかも呼ばれる

これ
等高線のグラフにして横から見る

上から
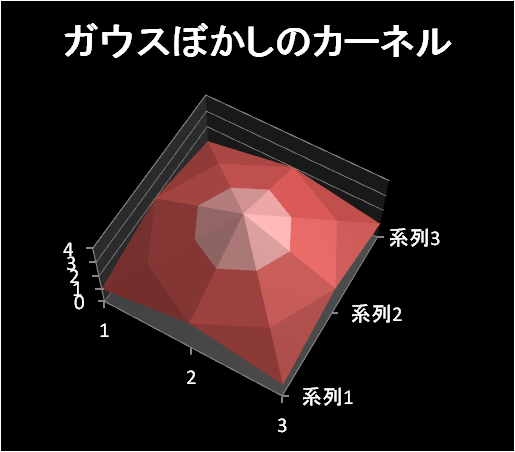
5x5のカーネルの場合
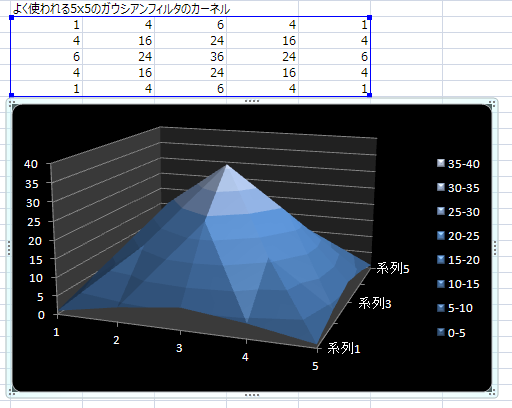
それも直線的に増えるんじゃないみたい
ここまでのカーネルは2次元、これが目的なんだけど、今回は1次元まで
画像のぼかし処理するだけならカーネルの数値さえ分かればいいんだけど
ググった先で読んでいると出てくるのが
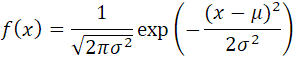
これ、さっぱりわからん
さらに混乱するのが微妙に違う式が同じようにあること
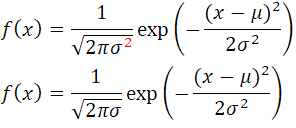
両方試して上の2乗されているほうがいい感じがしたので、上の式を使うことにして
まず記号のよみと意味がわからん
分数と√ルート、2乗はわかるとして、σとexpとμ
読み 意味 σ しぐま 標準偏差、σ^2は分散になる exp いーえっくすぴー 自然対数の底、だいたい2.7くらいの定数、エクセルの関数だと =EXP(1)で得られる。exponential(指数関数)の略 μ みゅー 平均
うーん、前に分散を使ったときはσじゃなくてアルファベットのsだったような
exp
エクセルにもそのままの名前EXP関数が用意されていて
expの右側が指数!
expは指数関数の略だっていうから
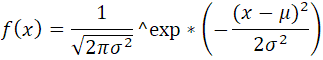
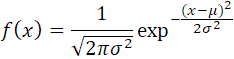
こういうことらしい
expって言われたらドラクエの経験値?くらいしか出てこない自分にしたら、わからんわ
エクセルやVBふうに書くと
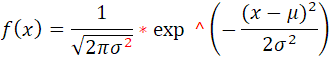
もっとエクセルらしく!
標準正規分布
ここまで見慣れない式と格闘してきたけどエクセルを使えば
エクセルのNORMDIST関数

エクセルにも用意されていた!
4つ目の引数はFalseを指定すると確率密度関数の答えになるので、今回はFalseを指定
このNORMDIST関数を使って

標準偏差=1のとき-1,0,1は1,2,1になった、こういうのが重みになるんだと思う
標準偏差=10にすると

標準偏差=0.5にすると

5x5のカーネルを考えて-2から2
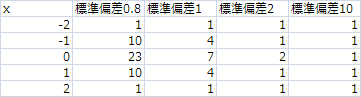
NORMDIST関数を使わずに計算してみる
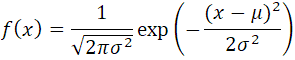
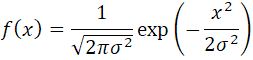
標準偏差=1のとき
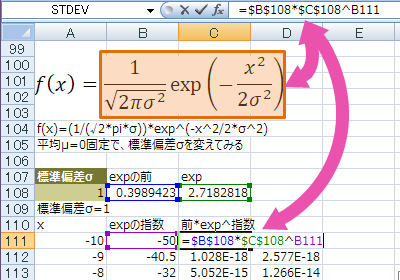
expの前の部分をエクセルで書くと
=1/SQRT(2*PI()*1^2)
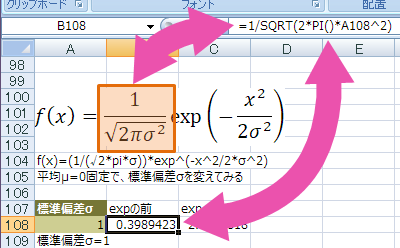
expの指数の部分は
=-(x^2/(2*1^2))
-(A111^2)/(2*$A$108^2)
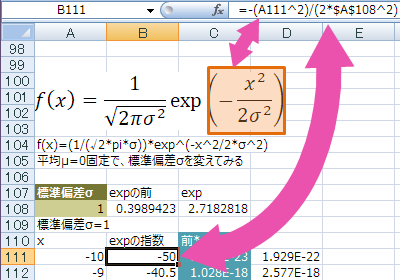
最後にまとめて
expの前*exp^指数
NORMDIST関数と比較
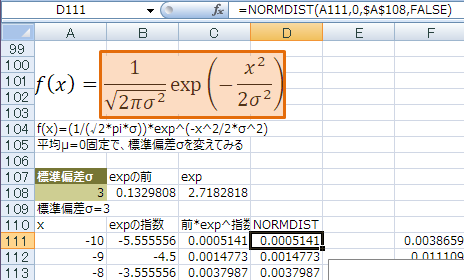
同じ値になった!
グラフにすると

標準偏差=3で、x=-10~10

ここまでは1次元
カーネルは縦横がある2次元は次回
参照したところ
関連記事
次回、2019/04/27
エクセルで2次のガウス関数(確率密度関数)、正規分布関数のNORMDIST ( ソフトウェア ) - 午後わてんのブログ - Yahoo!ブログ
https://blogs.yahoo.co.jp/gogowaten/15943071.html
2018/3/22は1年前
分割するCubeの選択、メディアンカットで減色パレット ( ソフトウェア ) - 午後わてんのブログ - Yahoo!ブログ分散は減色アプリのときが初めてだった
https://blogs.yahoo.co.jp/gogowaten/15425150.html
2019/05/22
画像にノイズ付加するアプリ、一様分布乱数から正規分布乱数生成、エクセルのNORMINV関数で正規乱数 ( ソフトウェア ) - 午後わてんのブログ - Yahoo!ブログ
https://blogs.yahoo.co.jp/gogowaten/15961286.html












