エクセルで2次のガウス関数(確率密度関数)、正規分布関数のNORMDIST
前回からの続き
変数xと変数yだった場合
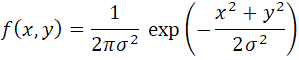
エクセルならNORMDIST関数2つの掛け算になって
=NORMDIST*NORMDIST
これだけ


等高線グラフにしてみると
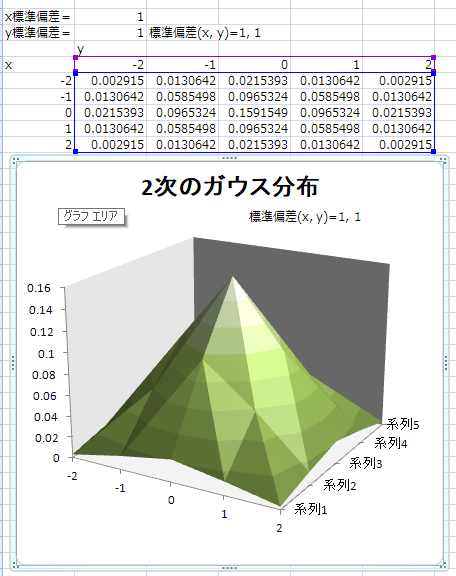
これは…前回の
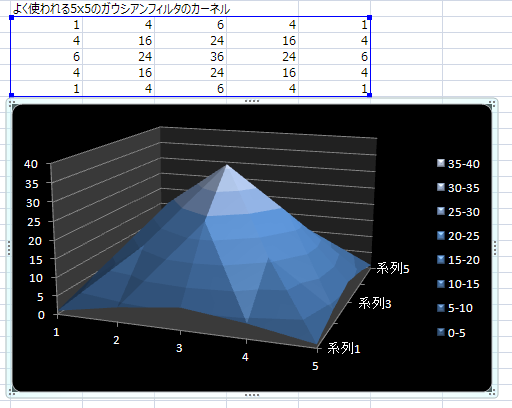
ガウシアンフィルタのカーネルにそっくり
もっとフィルタのカーネルっぽく
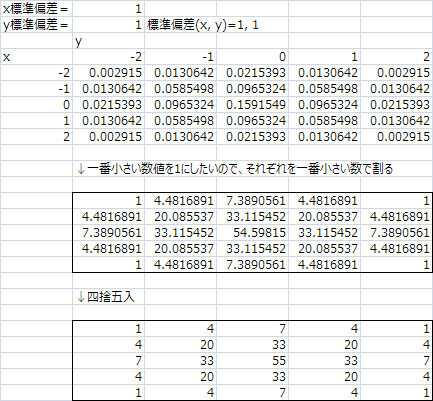
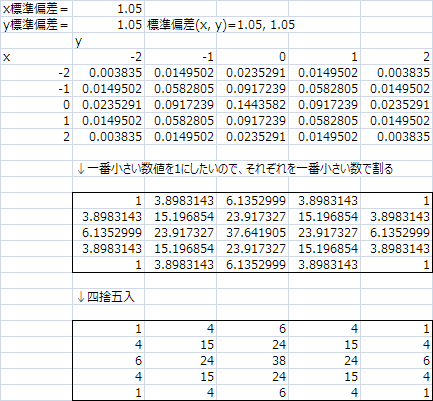
一番小さい数値でそれぞれを割って
四捨五入したらそれっぽくなった、もう少し
標準偏差を1.05に
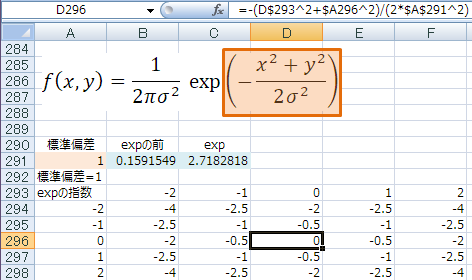
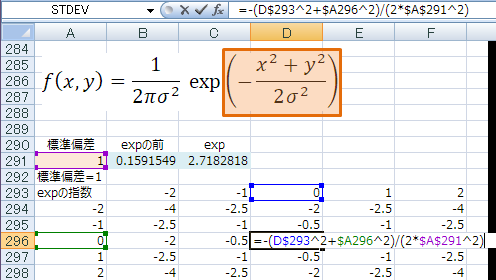
NORMDIST関数を使わずに計算してみる
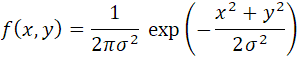
結果

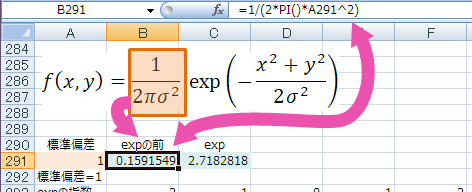
expの前だけ計算
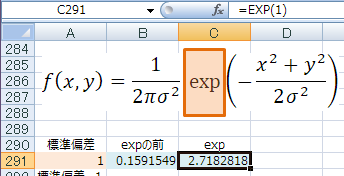
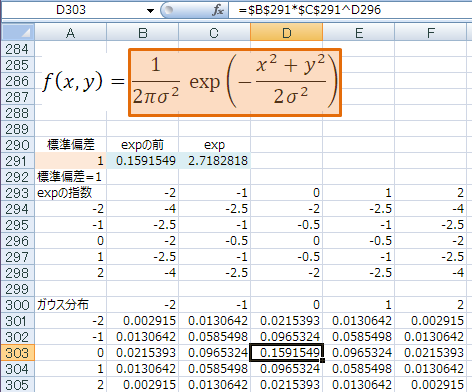
NORMDIST関数と同じ結果になった!
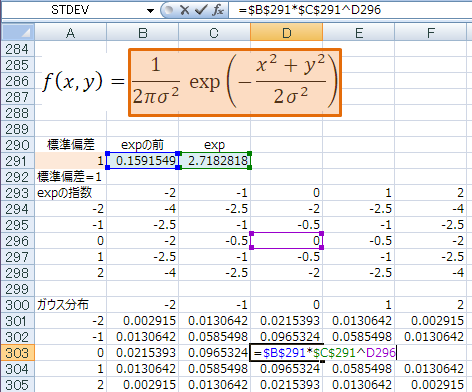

数値を整えてできた
1次から2次
2次の確率密度関数は1次同士を掛け算っていうことなので
こうで
それぞれの1次は
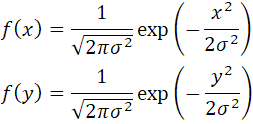
これを掛け算だから
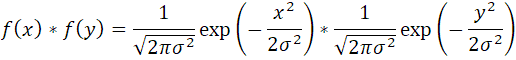
こうなって、これをうまい具合に計算する
普通に計算できそうなのはexpの前の分数同士の掛け算
分子同士、分母同士を掛け算して
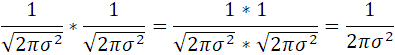
expの右側はexpの指数だからべき乗同士の掛け算は
忘れたのでぐぐったら指数法則で
元になる数値が同じなら指数同士の足し算、これに当てはまって
分数同士の足し算で
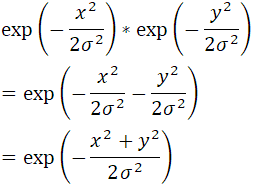
expの前とあわせて
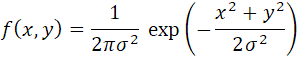
完成
こういう中学校レベルでもググらないと解けないとかね
ワード2007大活躍

もっと2次の正規分布っぽく!

標準偏差=0.5
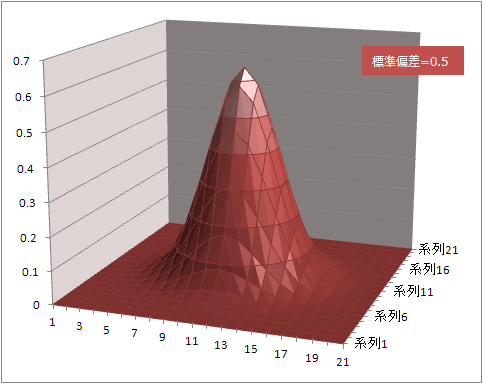
エクセルおもしろい
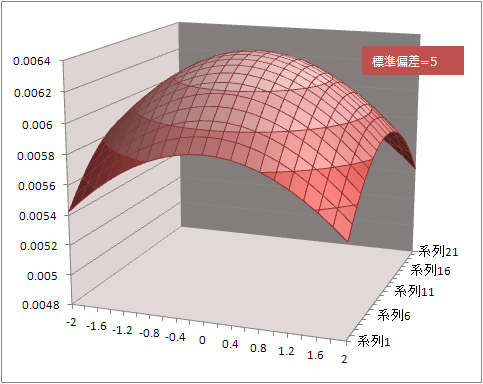
標準偏差=5
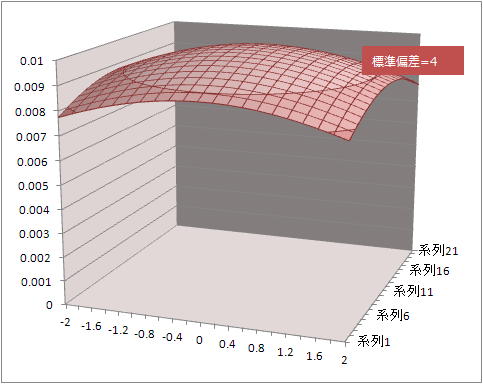
標準偏差=4
もう一度標準偏差=5
グラフの縦軸を標準偏差=4のグラフと同じ範囲0~0.01に変更
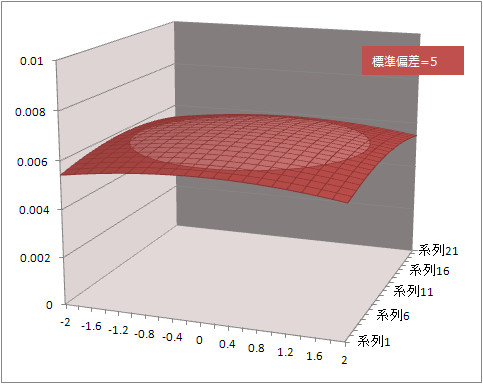
ちゃんとよりフラットになっていた
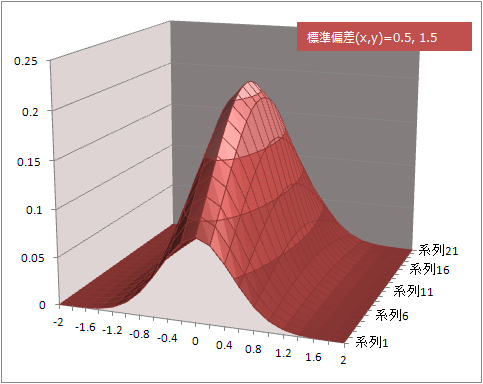
標準偏差をxとyで別々に指定
x=0.5, y=5
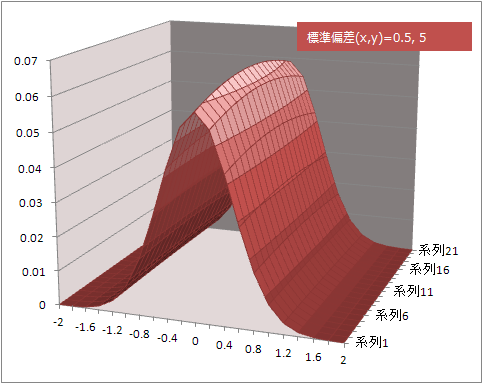
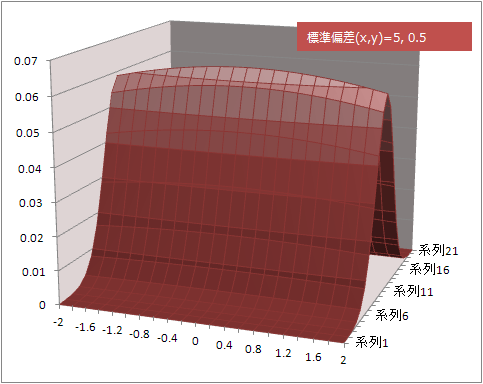
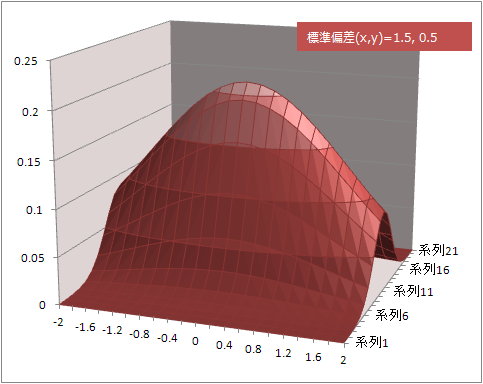
参照したところ
整式の乗法 [指数法則・指数の計算・累乗の計算] / 数学I by ふぇるまー |マナペディア|
http://manapedia.jp/text/2432
ガウシアンフィルタとバイラテラルフィルタ | 測度ゼロの抹茶チョコ
https://matcha-choco010.net/2018/07/01/%E3%82%AC%E3%82%A6%E3%82%B7%E3%82%A2%E3%83%B3%E3%83%95%E3%82%A3%E3%83%AB%E3%82%BF%E3%81%A8%E3%83%90%E3%82%A4%E3%83%A9%E3%83%86%E3%83%A9%E3%83%AB%E3%83%95%E3%82%A3%E3%83%AB%E3%82%BF/
関連記事
エクセルで1次のガウス関数(確率密度関数)、正規分布関数のNORMDIST ( ソフトウェア ) - 午後わてんのブログ - Yahoo!ブログ
https://blogs.yahoo.co.jp/gogowaten/15942730.html
次回、2019/04/30は3日後