午後わてんのブログ

ベランダ菜園とWindows用アプリ作成(WPFとC#)

Cubeから色の選び方、メディアンカットで減色パレット

WPF、C# .NET #ソフトウェア WPF ↓Windows用アプリ 画像処理 自作アプリ
2週間前の続き
 
 
ダウンロード先
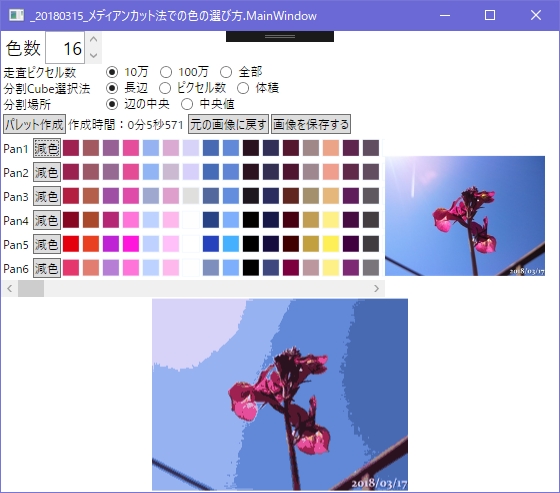
イメージ 1
メディアンカット法で分割したCubeからの色の選び方いろいろ試してみた
Pan1から6が選び方の違いで
Pan1 Cubeにあるピクセルの平均色
Pan2 CubeのRGBそれぞれの中央値(メディアン)
Pan3 Cubeの中心の色
Pan4 RGB空間の中心から見てCubeの中で一番遠い色
Pan5 Cubeの8隅の中でRGB空間の中心から見て一番遠い隅
Pan6 Cubeの中心から一番遠い色
 
CubeはRGB3要素(3軸)の直方体でエクセルだとうまくグラフにできないので
RBの2要素(2軸)の平面の長方形(rect)で
r b
215 250
124 226
76 190
155 247
123 52
73 193
129 248
104 231
29 24
イメージ 2
こういうピクセル9個の色があったとして
ここから4色に減色してみる
 
色の位置を
グラフにすると
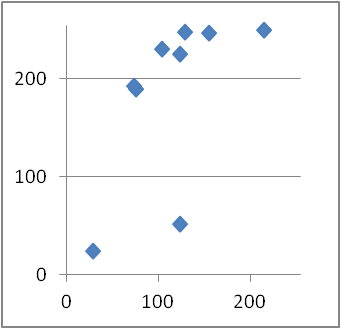
イメージ 4
こうなって
色の目安を重ねると
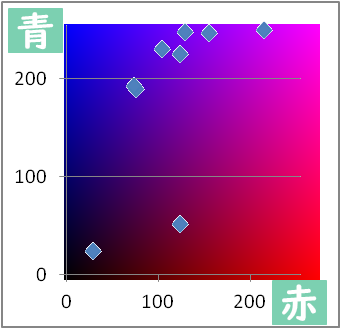
イメージ 3
横軸がR、縦軸がB
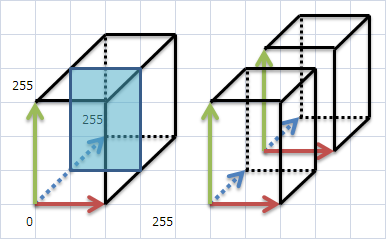
長方形の大きさは255ｘ255
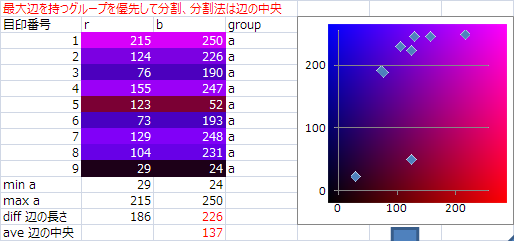
イメージ 5
長方形の余分なところを削る
RBのそれぞれの最小値と最大値の長方形にする
Rの最小値は29、最大値は215
Bの最小値は24、最大値は250
 
 
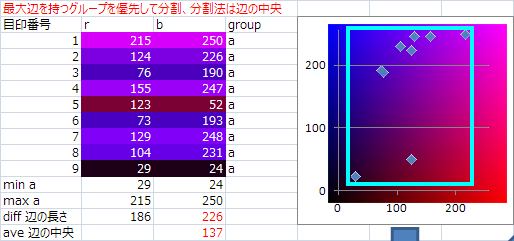
イメージ 6
水色枠が余分なところを削った長方形
これを分割する
 
分割する辺の選択
長い方の辺(軸)を分割する
Rの辺の長さは186
Bの辺の長さは226
なのでBを選択
 
辺の中心で分割する
B辺は24から250なので中心位置は
(250-24)/2+24=137
なので137の位置で分割すると
 
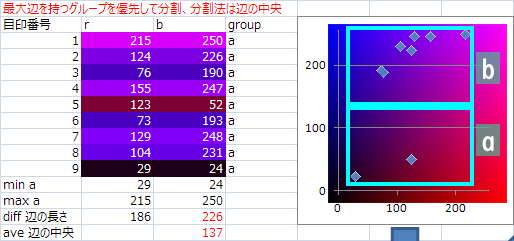
イメージ 7
グループaとbに分割
 
 

f:id:gogowaten:20191212123958p:plain

この時点で長方形が2つになったので2色パレットならここで分割終了になる
3色以上ならここから更に分割するので
どちらの長方形を分割するかの選択になる
 
今回は最大辺長を持つ方を優先分割する
グループaの最大辺長はR辺の94
グループbの最大辺長はR辺の142
なのでグループbを分割する
 
分割する辺の選択は長いほうなので
そのままR辺になる
分割場所は辺の中央なので
(215-73)/2+73=144
 
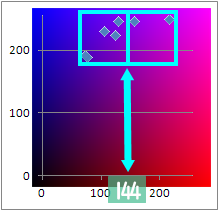
イメージ 10
グループbのR辺の144で分割して
グループbとc
 

f:id:gogowaten:20191212124012p:plain

これで3つまで分割できた、同じようにあと1回
最大辺長をもつグループaをR辺の中心76で分割して
 

f:id:gogowaten:20191212124027p:plain

4分割までできた
 
ここから4色を選ぶ
1.平均色
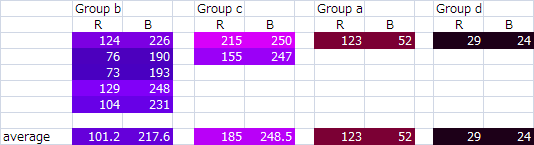
イメージ 12
グループaとdは1色しか入っていないのでこれで確定
b,cの平均色を求める
RBそれぞれの平均を組み合わせた色を平均色としてみた
なので元になったピクセルにはない色になる場合もある
グループbの平均色は101,217になったけど
元のピクセルにはない色
 
この方法はすべてのピクセルとの計算だけど
全部足して1回割るだけだからそんなに時間はかからないかな
以前の記事では、すべてこの方法で選んでいた
 
 
2.中央値(メディアン)で選ぶ
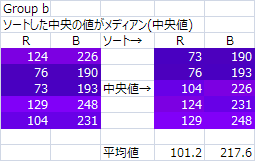
イメージ 13
グループbの場合
RBそれぞれを並べ替えて中央の位置にあるもの
RB(104,226)が中央値になる
もし要素数が偶数の場合は中央2つの平均値
例えば10,20,30,40,50,100という要素数6なら
30と40が中央の2つなので
(30+40)/2
=35
 
中央値って平均値とはまた別なんだよねえ
同じだと思ってた
そんな感じであんまりわかっていないけど
並べ替えが意外に重たい処理
それでも平均色よりは軽そう
 
 
 
3.RBの中心(127.5,127.5)から遠い色を選ぶ
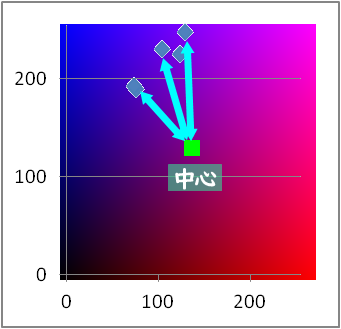
イメージ 14
ユークリッド距離で比較
 
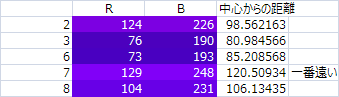
イメージ 15
7番が一番遠かった
(127.5-129)^2+(127.5-248)^2=14522.5
これの平方根が√14522.5=120.50934
 
この方法はすべてのピクセルの色との計算をするから
色の選び方の中では一番時間がかかる
 
遠い色を選んだのは
そのほうが極端な色(鮮やかな色)になって面白そうだと思ったから
中心に近い色だと灰色に近くなるし
平均色とも近くなるかなあと
でも近いのも試してみればよかった
 
 
 
4.長方形の4隅の中で一番RBの中心から遠い隅
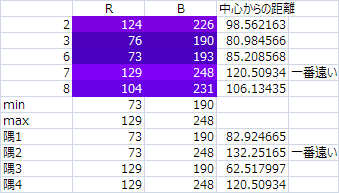
イメージ 17
四隅の座標は最小値、最大値の組み合わせ
中心からのユークリッド距離
一番遠かった隅2だと
(127.5-73)^2+(127.5-248)^2=17490.5
これの平方根は√17490.5=132.21565
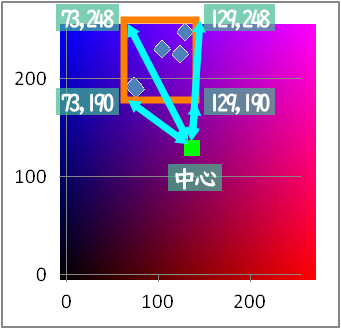
イメージ 16
見た目からも左上の隅(73,248)が一番遠い
この選び方はさっきのより極端な色になるはず
この方法は4点との計算だからラク
 
 
5.長方形の中心から一番遠い色
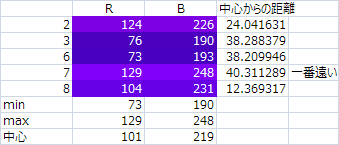
イメージ 19
これもユークリッド距離
この方法もすべてのピクセルとの計算だから時間がかかる
 

f:id:gogowaten:20191212124120p:plain

一番遠かったのは右上の7番(129,248)
 
 
6.長方形の中心

f:id:gogowaten:20191212124101p:plain

緑の四角のあたりの色R,B(101,219)
長方形の中心なので元のピクセルにはない色になることもある
これは一回の計算で済むからラク
 
 
以上の6通りの方法での減色パレットを
イメージ 21
この画像から4色
RGBなのでCube(直方体)で計算して
 
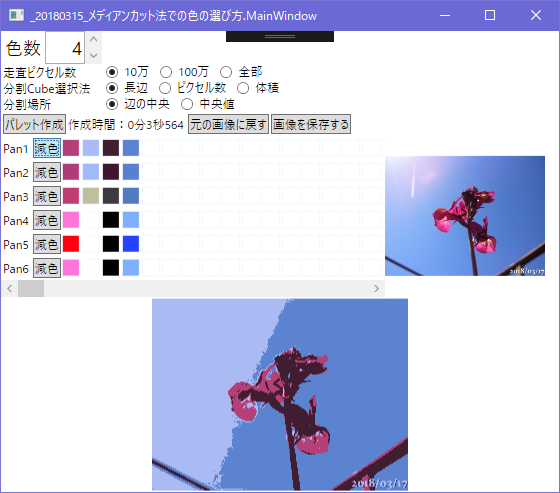
イメージ 22
p5は派手な色が並んだ
 
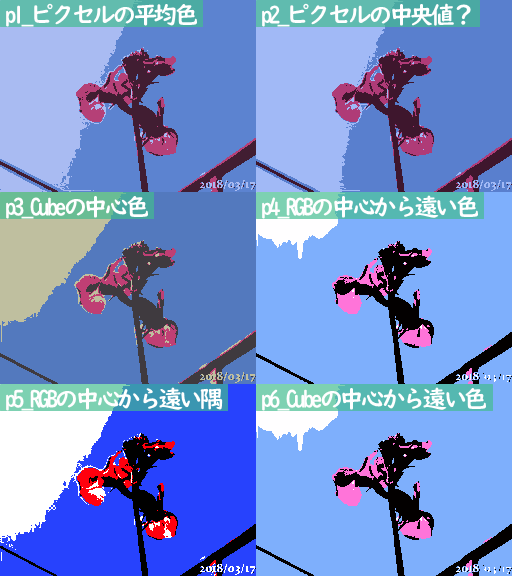
イメージ 23
p1の平均色は今までどおりの見慣れた無難なパレット
p2の中央値パレットは平均色とほぼ同じ色になった
p3は灰色っぽいくすんだ、中心って感じのパレット
p4とp6は全く同じ色になった、鮮やかな色
p5は予想通りの極端な色、白と黒は見たままの色だけど
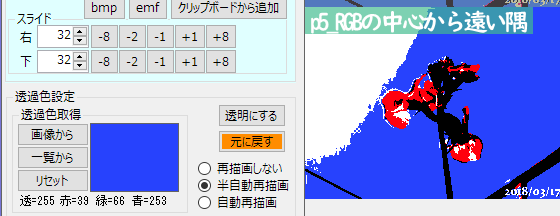イメージ 24
青は39,66,253、赤も真っ赤じゃなくて255,0,14だった
こういう極端な色はディザリングや誤差拡散を使うと良くなると思う
 
 
16色パレット
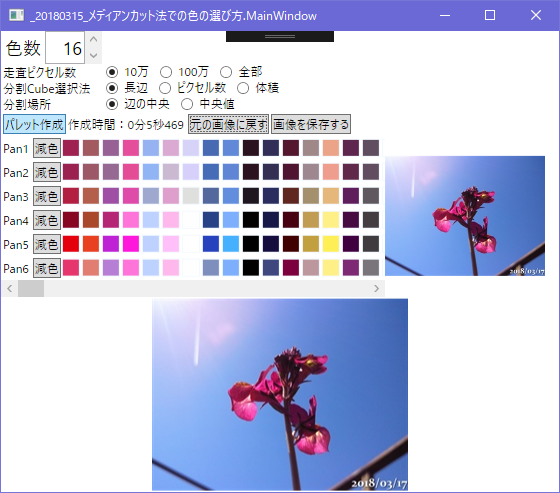
イメージ 25
イメージ 26
4色のときは同じだったp4とp6はかなり違う色になった
p1,2は安定している感じ
そしてp5の極端さ
 
256色
イメージ 27
左端から右端まで256色
どのパレットも同じ色が並んでいるように見える
けど
イメージ 28
変換して並べてみると違った
それでも1枚1枚出されたら見分けつかないなあ
256色も使えばもっときれいになるかと思ったけど
どれも青空のグラデーションの縞模様が出ているねえ
花の部分は元画像と区別つかないくらい、きれいに減色できている
 
 
 
分割するCubeの選択方法を最大ピクセルに変更すると
縞模様が軽減される
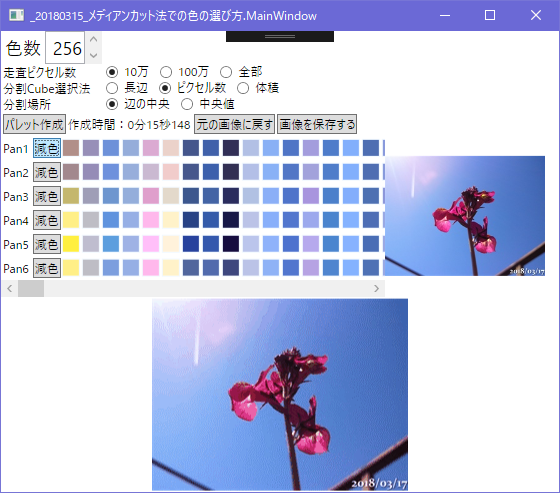
イメージ 29
さっきまでは分割するCubeの選択方法は最大辺長を持つCubeだった
これを最大ピクセル数を持つCubeに変更してパレットを作ると
ピクセル数の多い青空にパレットが割り振られて
縞模様が出にくくなる
同じ256色でもぜんぜん違う
 
 
8色
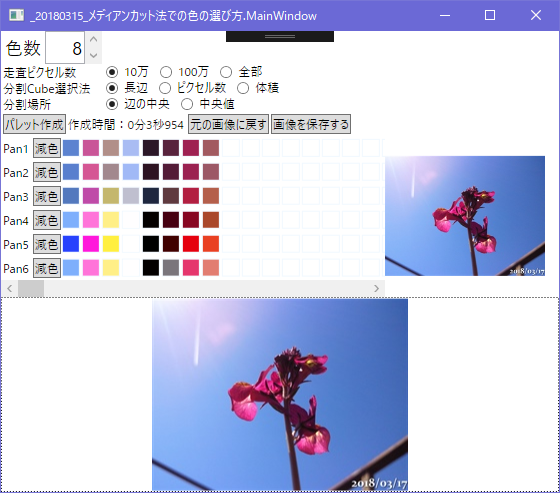
イメージ 30
イメージ 31
p4がきれい
 
 
別の画像で4色
イメージ 32
p3、やっぱり中心に近いとくすんだ色になるねえ
遠いほど鮮やかな色になる、p5,4,6は誤差拡散が楽しみ
 
 
16色
イメージ 33
p4,5,6の変換がいまいち、パレットにはもっといい色があるのに使われていないのは色の距離をRGBのユークリッド距離で測っているから、これはなんとかしたいけど難しい
 
 
4色
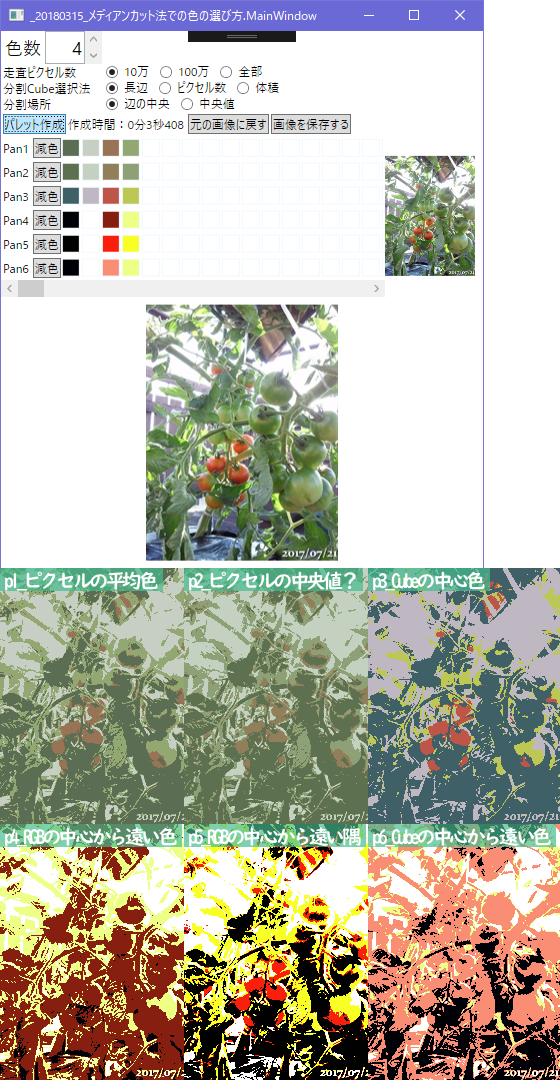
イメージ 34
p1,2の安定とp4,5,6の不安定さ
普通に減色したいだけならp1の平均色がいいね
 
16色
イメージ 35
p1,2はここまでほとんど差がないからどちらかがあれば良さそう
p3珍しく派手になっている
p4,5,6はおかしいｗ色の距離がなあ
 
 
32色
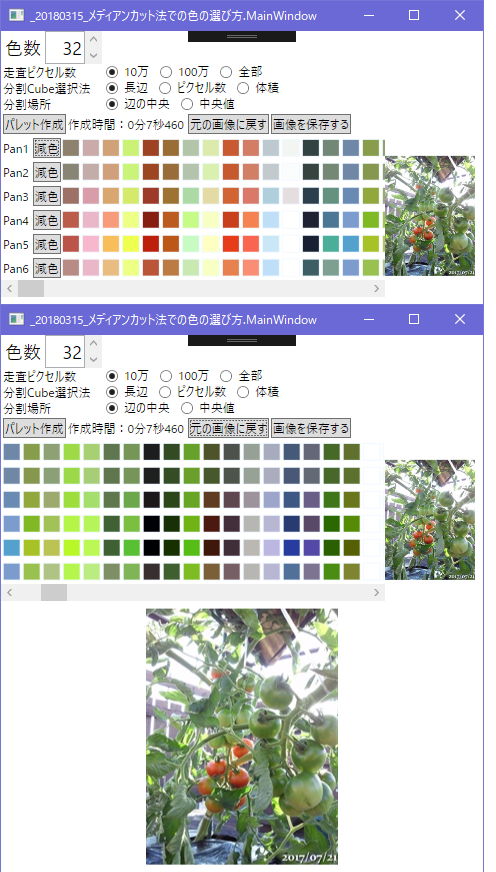
イメージ 36
32色まで増やすと緑系もたくさん配置されて
イメージ 37
だいぶ落ち着く
 
グラデーション画像
4色
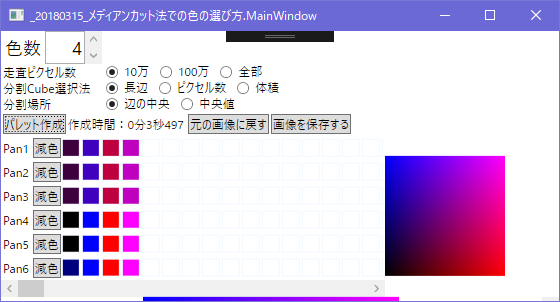
イメージ 38
イメージ 43
p1とp2、p3が全く同じ色
p4とp5も全く同じ色(0,0,255)(255,0,255)(0,0,0)(255,0,0)の4色で
どちらも期待どおり！
 
 
16色
イメージ 44
イメージ 45
4色と同じくp1とp2,p3、p4とp5が同じ色のパレットになった
 
256色
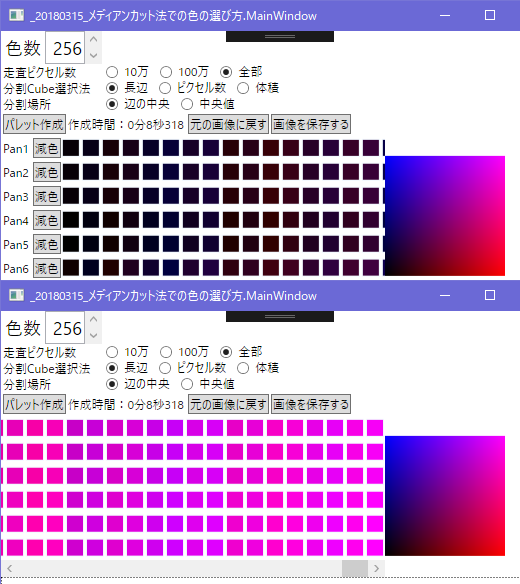
イメージ 46
イメージ 47
グラデーション画像はp6が他とは違うねえ
中央が誤差拡散したみたいになっている

f:id:gogowaten:20191212124226p:plain

 
色相90のHSVグラデーション画像
4色
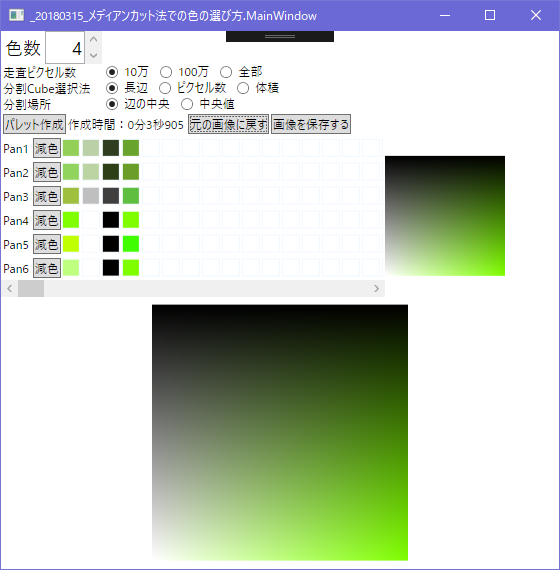
イメージ 39
イメージ 40
p4は3色に見えるけど4色使っているらしい
 
16色
イメージ 41
256色
イメージ 42
256色だと違うのはわかるけど違いがわからない
 
感想
Pan1 Cubeにあるピクセルの平均色
Pan2 CubeのRGBそれぞれの中央値(メディアン)
Pan3 Cubeの中心の色
Pan4 RGB空間の中心から見てCubeの中で一番遠い色
Pan5 Cubeの8隅の中でRGB空間の中心から見て一番遠い隅
Pan6 Cubeの中心から一番遠い色
 
p1,2は似た傾向で最も良い結果、元の画像に近い
p3は地味め
p4,5も似た傾向でどちらも派手で極端なパレットになる
p6は4,5を少し抑えた感じ
どれか一つを選ぶとすればp1かp2で迷ってp1
もう一つ選べるならp5！誤差拡散時に期待
 
処理の重たさは測っていないけど書いた感じは
4=6>1≒2>>5>3
かな5,3は一瞬で終わるはず、4と6はピクセル数に比例するので画像のサイズが大きいほど時間がかかる、1と2もそうだけどもう少し軽いはず
 
256色とか色数が多くなると差がなくなる、面白いのは4～32色くらいかな
 
 
 
コードの一部
/// <summary>
/// RGBそれぞれの最小値と最大値を持つクラス
/// その他にRGBそれぞれの辺の長さ、画像の全ピクセルの色、使用されている色を持つ
/// コンストラクタはbitmapSourceかColorのListから作成するものだけ、それだけのクラス
/// </summary>
public class Cube
{
    public byte MinRed;//最小R
    public byte MinGreen;
    public byte MinBlue;
    public byte MaxRed;//最大赤
    public byte MaxGreen;
    public byte MaxBlue;
    public List<Color> AllPixelsColor;//すべてのピクセルの色リスト     
    public List<Color> AllColor;//使用されているすべての色リスト
    public int LengthMax;//Cubeの最大辺長
    public int LengthRed;//赤の辺長
    public int LengthGreen;
    public int LengthBlue;

    //BitmapSourceからCubeを作成
    public Cube(BitmapSource source)
    {
        var bitmap = new FormatConvertedBitmap(source, PixelFormats.Pbgra32, null, 0);
        var wb = new WriteableBitmap(bitmap);
        int h = wb.PixelHeight;
        int w = wb.PixelWidth;
        int stride = wb.BackBufferStride;
        byte[] pixels = new byte[h * stride];
        wb.CopyPixels(pixels, stride, 0);
        long p = 0;
        byte cR, cG, cB;
        byte lR = 255, lG = 255, lB = 255, hR = 0, hG = 0, hB = 0;
        AllPixelsColor = new List<Color>();
        for (int y = 0; y < h; ++y)
        {
            for (int x = 0; x < w; ++x)
            {
                p = y * stride + (x * 4);
                cR = pixels[p + 2]; cG = pixels[p + 1]; cB = pixels[p];
                AllPixelsColor.Add(Color.FromRgb(cR, cG, cB));
                if (lR > cR) { lR = cR; }
                if (lG > cG) { lG = cG; }
                if (lB > cB) { lB = cB; }
                if (hR < cR) { hR = cR; }
                if (hG < cG) { hG = cG; }
                if (hB < cB) { hB = cB; }
            }
        }
        //重複を除いて使用されている色リスト作成、Distinct
        //IEnumerable<Color> result = AllPixelsColor.Distinct();
        AllColor = AllPixelsColor.Distinct().ToList();//これの処理コストが結構大きい

        MinRed = lR; MinGreen = lG; MinBlue = lB;
        MaxRed = hR; MaxGreen = hG; MaxBlue = hB;
        LengthRed = 1 + MaxRed - MinRed;
        LengthGreen = 1 + MaxGreen - MinGreen;
        LengthBlue = 1 + MaxBlue - MinBlue;
        LengthMax = Math.Max(LengthRed, Math.Max(LengthGreen, LengthBlue));
    }

    //ColorのリストからCube作成
    public Cube(List<Color> color)
    {
        byte lR = 255, lG = 255, lB = 255, hR = 0, hG = 0, hB = 0;
        byte cR, cG, cB;
        AllPixelsColor = new List<Color>();
        foreach (Color item in color)
        {
            cR = item.R; cG = item.G; cB = item.B;
            AllPixelsColor.Add(Color.FromRgb(cR, cG, cB));
            if (lR > cR) { lR = cR; }
            if (lG > cG) { lG = cG; }
            if (lB > cB) { lB = cB; }
            if (hR < cR) { hR = cR; }
            if (hG < cG) { hG = cG; }
            if (hB < cB) { hB = cB; }
        }
        //重複を除いて使用されている色リスト作成、Distinct
        AllColor = AllPixelsColor.Distinct().ToList();//これの処理コストが結構大きい

        MinRed = lR; MinGreen = lG; MinBlue = lB;
        MaxRed = hR; MaxGreen = hG; MaxBlue = hB;
        LengthRed = 1 + MaxRed - MinRed;
        LengthGreen = 1 + MaxGreen - MinGreen;
        LengthBlue = 1 + MaxBlue - MinBlue;
        LengthMax = Math.Max(LengthRed, Math.Max(LengthGreen, LengthBlue));
    }
}


//Cubeから色の選び方6通り

//p1.平均色、Cubeの中心の色じゃなくてピクセルの平均
public Color GetColorCubeAverage平均色(Cube cube)
{
    List<Color> colorList = cube.AllPixelsColor;
    long r = 0, g = 0, b = 0;
    int cCount = colorList.Count;
    if (cCount == 0)
    {
        return Color.FromRgb(127, 127, 127);
    }

    for (int i = 0; i < cCount; ++i)
    {
        r += colorList[i].R;
        g += colorList[i].G;
        b += colorList[i].B;
    }
    return Color.FromRgb((byte)(r / cCount), (byte)(g / cCount), (byte)(b / cCount));
}



//p2.RGBそれぞれの中央値(メディアン)
private Color GetColorCubeMedian(Cube cube)
{
    var r = new List<byte>();
    var g = new List<byte>();
    var b = new List<byte>();

    foreach (Color item in cube.AllPixelsColor)
    {
        r.Add(item.R);
        g.Add(item.G);
        b.Add(item.B);
    }
    r.Sort();
    g.Sort();
    b.Sort();

    if (r.Count % 2 == 0)
    {
        int back = r.Count / 2;
        return Color.FromRgb(
            (byte)((r[back] + r[back - 1]) / 2),
            (byte)((g[back] + g[back - 1]) / 2),
            (byte)((b[back] + b[back - 1]) / 2));
    }
    else
    {
        int median = (cube.AllPixelsColor.Count - 1) / 2;
        return Color.FromRgb(r[median], g[median], b[median]);
    }
}



//p3.Cubeの中心の色を返す、面白い
public Color GetColorCubeCore中心色(Cube cube)
{
    byte r = (byte)((cube.MaxRed - cube.MinRed) / 2 + cube.MinRed);
    byte g = (byte)((cube.MaxGreen - cube.MinGreen) / 2 + cube.MinGreen);
    byte b = (byte)((cube.MaxBlue - cube.MinBlue) / 2 + cube.MinBlue);
    return Color.FromRgb(r, g, b);
}


//p4.Cubeの中心から一番遠いピクセルの色
private Color GetColorCubeDistantCore(Cube cube)
{
    float rCore = (cube.MaxRed - cube.MinRed) / 2f;
    float gCore = (cube.MaxGreen - cube.MinGreen) / 2f;
    float bCore = (cube.MaxBlue - cube.MinBlue) / 2f;
    double distance;
    double max = 0;

    Color distantColor = Colors.Black;
    foreach (Color item in cube.AllColor)
    {
        distance = GetColorDistance(rCore, gCore, bCore, item);
        if (max < distance)
        {
            max = distance;
            distantColor = item;
        }
    }
    return distantColor;
}



//p5.Cubeの8隅のうちRGB空間の中心から一番遠い隅
private Color GetColorCubeDistantVertexRGBCore(Cube cube)
{
    double distance;
    double max = 0;
    int lIndex = 0;
    var corner8 = new Color[]//8隅の色
    {
        Color.FromRgb(cube.MinRed,cube.MinGreen,cube.MinBlue),
        Color.FromRgb(cube.MinRed,cube.MinGreen,cube.MaxBlue),
        Color.FromRgb(cube.MinRed,cube.MaxGreen,cube.MinBlue),
        Color.FromRgb(cube.MaxRed,cube.MinGreen,cube.MinBlue),
        Color.FromRgb(cube.MinRed,cube.MaxGreen,cube.MaxBlue),
        Color.FromRgb(cube.MaxRed,cube.MinGreen,cube.MaxBlue),
        Color.FromRgb(cube.MaxRed,cube.MaxGreen,cube.MinBlue),
        Color.FromRgb(cube.MaxRed,cube.MaxGreen,cube.MaxBlue),
    };

    for (int i = 0; i < corner8.Length; ++i)
    {
        distance = GetColorDistance(127.5, 127.5, 127.5, corner8[i]);
        if (max < distance)
        {
            max = distance;
            lIndex = i;
        }
    }
    return corner8[lIndex];
}


//p6.CubeのピクセルのうちRGB空間の中心から一番遠いピクセルの色
private Color GetColorCubeDistantRGBCore(Cube cube)
{
    double distance;
    double max = 0;

    Color distantColor = Colors.Black;
    foreach (Color item in cube.AllColor)
    {
        distance = GetColorDistance(127.5, 127.5, 127.5, item);
        if (max < distance)
        {
            max = distance;
            distantColor = item;
        }
    }
    return distantColor;
}
 
 
 
 
 
 
参照したところ
 
C# で高階関数的な、関数ポインタみたいな（Func でメソッドを切り替える） - 学び、そして考える
http://d.hatena.ne.jp/p-nix/20090226/p1
関数を引数として渡す、引数として関数を渡す方法、Func
今回初めて使ってみた、便利！
 
 
 
減色の処理で使う中央値や分散、偏差は統計っていうジャンル？らしい、習った憶えないんだよなあ、さすがの記憶力！と思っていたら
なんでも今度から文系学校の数学からベクトルが消えて、代わりに統計になるとかで、つまり今までは統計を教えていなかったみたいで、ああ、やっぱり習ってなかったんだって少し安心したｗ普通科ってのは文系だったんだなあ、たしかに時間割で理系は少なかった。
ベクトルは担当の先生が面白い方だったから楽しかったけど、今まで使う場面が殆どなかったからなあ
統計に切り替えるのはパソコン(計算機)との相性が良いからだろうねえ、手書きで計算してもめんどくさいだけだけどパソコン使えば楽ちんは楽しい。
 
 
コード全部
 
アプリダウンロード
 
 
関連記事
2018/03/22、今回の記事の続き
分割するCubeの選択、メディアンカットで減色パレット ( ソフトウェア ) - 午後わてんのブログ - Yahoo!ブログ
https://blogs.yahoo.co.jp/gogowaten/15425150.html
 
 
2018/3/6は2週間前
メディアンカット法で色の選択、減色してみた、難しい ( ソフトウェア ) - 午後わてんのブログ - Yahoo!ブログ
https://blogs.yahoo.co.jp/gogowaten/15400162.html
 
関連記事
2019/03/01は1年後
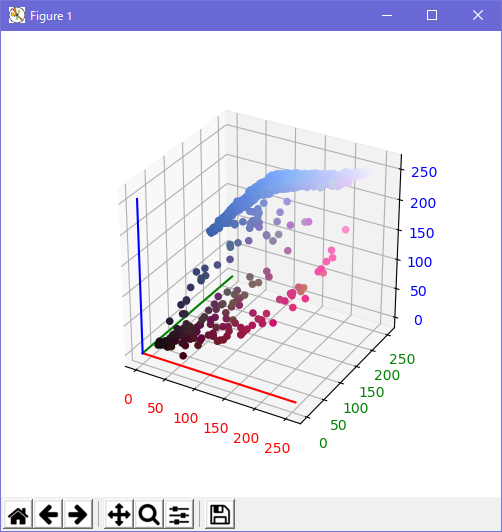
画像で使われている色を3D散布図で表示してみた、Pythonとmatplotlibすごい ( ソフトウェア ) - 午後わてんのブログ - Yahoo!ブログ
https://blogs.yahoo.co.jp/gogowaten/15887088.html
https://blog-001.west.edge.storage-yahoo.jp/res/blog-96-35/gogowaten/folder/578471/88/15887088/img_25_m?1551369038